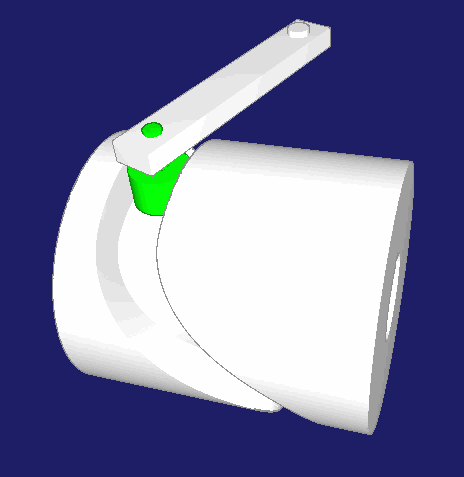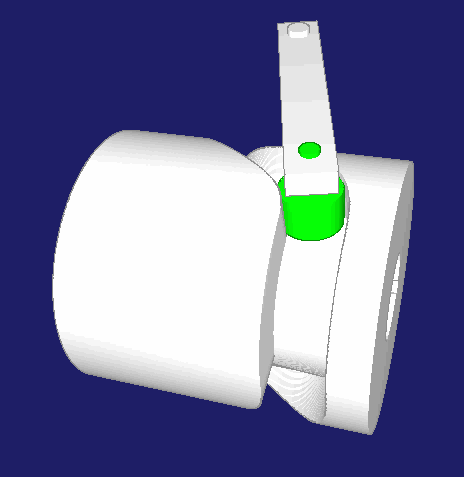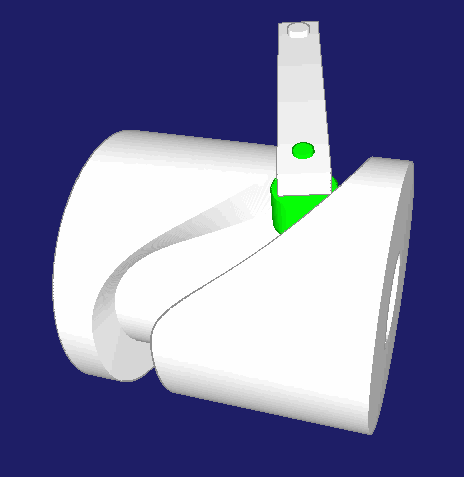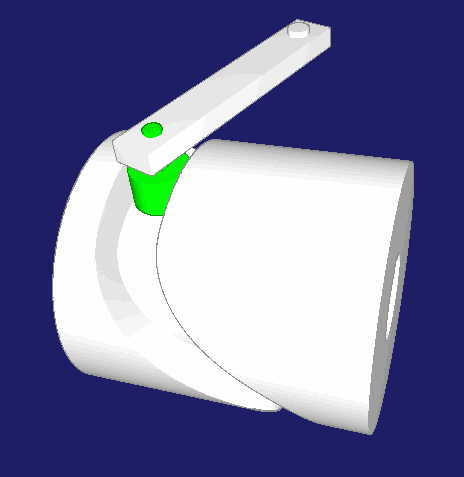
Zylinderkurven
Zylinderkurven sind neben Kurvenscheiben und Globoidkurven eine verbreitete Bauform von Kurven. Zylinderkurven werden verwendet, wenn die Abtriebsbewegung im Wesentlichen parallel zur Kurvendrehachse laufen soll. Im Gegensatz dazu bewegt sich der Abtrieb bei Kurvenscheiben in der Regel senkrecht zur Kurvendrehachse bzw. zur Antriebsachse.
Mechanismen werden gerne so einfach wie möglich gebaut, mit möglichst wenigen Teilen und Gelenken, um Spiel und Elastizität gering zu halten. Bei einer Antriebswelle mit mehreren Kurven wird man zwar alle Bewegungen mit Kurvenscheiben steuern können, aber für die Abtriebsbewegungen parallel zur Kurvendrehachse wird man dann räumliche Koppelgetriebe zur Bewegungs-Umlenkung einsetzen müssen. Die Gelenkköpfe darin haben Spiel und schaden der Dynamik der Maschine. Deshalb ist es oft besser, solche Bewegungen parallel zur Kurvendrehachse direkt von einer Zylinderkurve abzunehmen.
Gerne berechnen und optimieren wir Zylinderkurven für Sie und stellen Ihnen Fertigungs- und CAD-Daten zur Verfügung.
Zylinderkurven werden auch oft in Schrittgetrieben verwendet. Dabei gibt es zwei Varianten:
- konstante Drehzahl am Antrieb und eine Übertragungsfunktion für die Schrittbewegung
- Übertragungsfunktion mit konstanter Steigung ("Zylinderschnecke") und gesteuerter Antrieb mit Servomotoren
Auch im zweiten Fall ist es erforderlich, die Form der Kurvenflanken mit einer Kurvenberechnung korrekt zu ermitteln, weil sich die konstante Steigung in der Regel auf die Drehbewegung des Abtriebsrades bezieht! Zylinderkurven mit konstanter Steigung am Abtrieb entsprechen nicht einer Spindel mit konstanter Steigung, bei denen die Rollen linear direkt über der Kurvenachse laufen!
Weiterhin werden feststehende Zylinderkurven mit mehreren umlaufenden Abgriffen häufig in Rundläufer-Maschinen verwendet:
Die Artikel, oft Flaschen oder Dosen, werden dabei meanderförmig um mehrere Karussells herum geführt. Bei voller Durchlaufgeschwindigkeit können beispielsweise Flaschen befüllt, mit Kappen verschlossen oder etikettiert werden. Dosen können geformt, befüllt und gebördelt werden.
Im Durchlaufbetrieb entsteht ein sehr hoher Durchsatz.
Vorteile von Zylinderkurven:
- Bewegungen parallel zur Antriebsachse direkt abgreifbar,
- dabei kompakte und steife Bauweise
- hohe Schwungmasse (Vorteil bei konstanter Antriebsdrehzahl)
Nachteile von Zylinderkurven:
- hohe Eigenträgheit (Nachteil bei Antrieb mit Servo oder Not-Stop)
- schwieriger herzustellen (4- bzw. 5-achsige Bearbeitung), damit teurer
- komplizierte räumliche Geometrie der Kurvenflanke, muss bei Austragungen im 3D-CAD beachtet werden
- in der Regel immer auch Gleitanteil beim Abwälzen der Rolle auf der Kurve, begünstigt Verschleiß
Die räumliche Geometrie ist bei Zylinderkurven nicht trivial. Kurvenscheiben sind in dieser Hinsicht viel einfacher zu handhaben.
Wir berechnen Zylinderkurven seit Jahrzehnten und kennen die damit verbundenen speziellen Fragen (und Antworten) aus dem Eff-Eff.
Gerne unterstützen wir Sie bei der Auslegung Ihrer Zylinderkurven und bei der Erstellung exakter NC- und CAD-Daten mit unserer Software OPTIMUS MOTUS oder unseren Beratungs- und Berechnungsdienstleistungen.
Gerne nehmen wir auch direkt Kontakt mit Ihrer Fertigung auf, wenn Fragen zur Verwendung der Daten aufkommen sollten.
Direkt zu ...
- Abwicklungsdarstellung
- Koordinatensysteme
- Herstellung
- Fasen
- CAD-Aufbereitung
- Fehlermöglichkeiten
- spezielle Bauformen
zur Startseite von Nolte NC-Kurventechnik GmbH
> English version of this page
Abwicklungsdarstellung
Auf Zeichnungen oder für Berechnungen ist es üblich, Zylinderkurven in der Abwicklungsdarstellung zu betrachten, auch kurz "Abwicklung" genannt. Dabei werden die räumlichen Kurvenbahnen in die Ebene gestreckt. Für die Abwicklung wird die Kurve von außen betrachtet.
Die Abwicklungsdarstellung ist also die in die Ebene ausgestreckte Ansicht des Kurvenmantels von außen.
Das folgendes gedankliche Bild soll das erläutern:
Man nehme eine Flasche mit Etikett und zeichne mit einem Filzschreiber ringsherum eine beliebige "Kurvenbahn" darauf. Dann nehme man ein Messer und schneide das Etikett an irgendeiner Stelle quer durch, also in Längsrichtung der Flasche. Wenn das Etikett nicht aufgeklebt ist, hat man jetzt zwei lose Enden, die man straff ziehen kann, bis das Etikett ganz gerade gestreckt ist und tangential an der Flasche anliegt. Betrachtet man nun die anfangs gezeichnete Kurvenbahn, sieht man die Abwicklungsdarstellung.
Die folgende Animation zeigt das an einem Beispiel:
- links in räumlicher Darstellung
- rechts daneben in Abwicklungsdarstellung
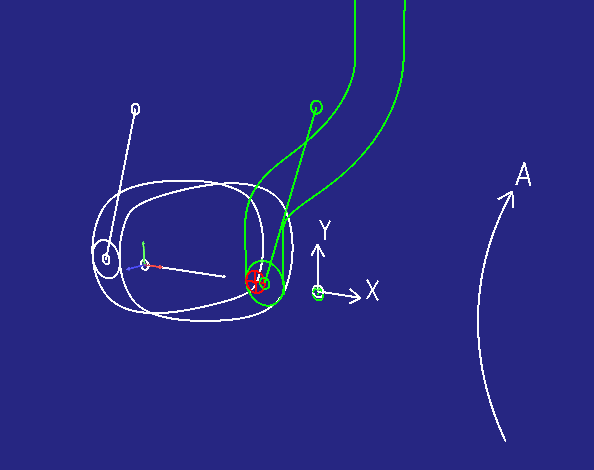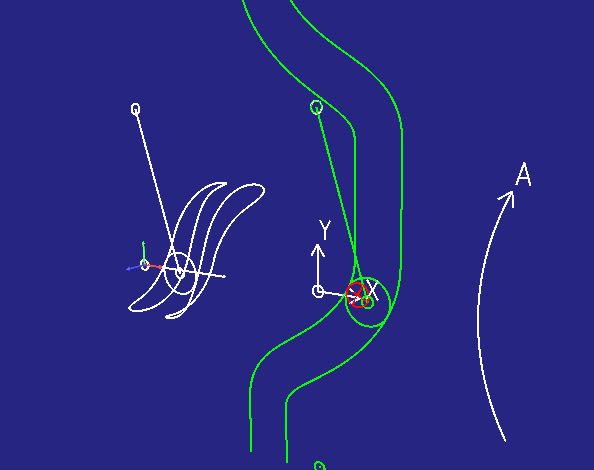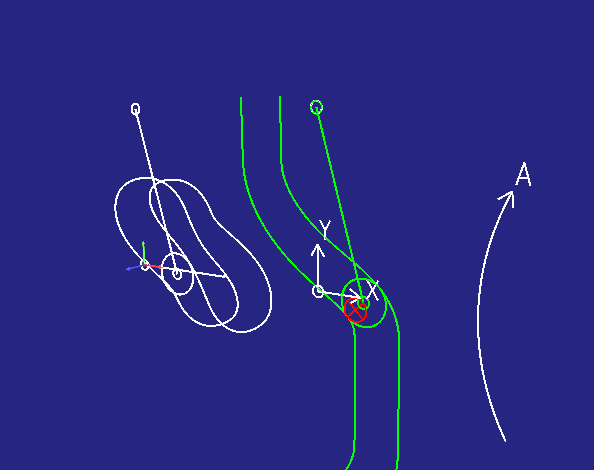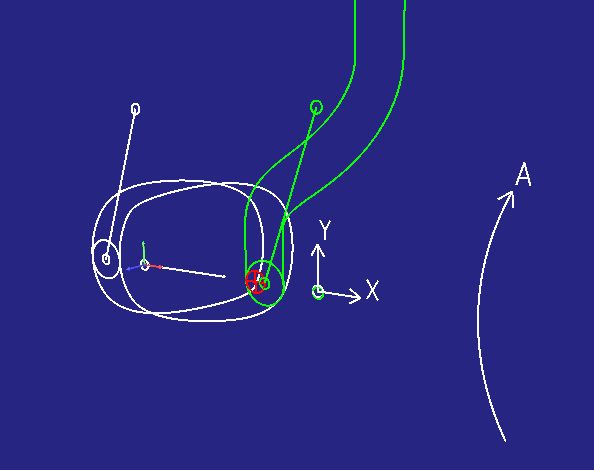
Der kleinere rote Kreis stellt ein Werkzeug dar, mit dem man die Kurvenbahnen fräsen möchte. Die Abwicklungsdarstellung kann für die Berechnung einer Werkzeugradius-Korrektur verwendet werden.
Die Abwicklungsdarstellung bezieht sich auf einen festgelegten Durchmesser D auf der Kurve.
Intuitiv wird dabei oft der Außendurchmesser der Kurve bzw. der Kurvenflanke verwendet. Zur Erhöhung der Fertigungsgenauigkeit ist es aber besser, als Bezugsdurchmesser den Wirkdurchmesser zu verwenden. Das ist der Durchmesser an der Kurve, auf dem die in der Regel ballige Rolle theoretisch Kontakt mit der Kurve hat, und zwar wenn der Kontaktpunkt in der Bewegungsebene des Abtriebs genau über der Kurvendrehachse liegt. Ersatzweise eignet sich auch der mittlere Durchmesser der Kurvenflanke sehr gut als Bezugsdurchmesser.
Die Abwicklungsdarstellung hat eine Länge von D•pi.
Flanken von Zylinderkurven stehen quasi auf dem Kurvenmantel und überstreichen dabei einen Durchmesserbereich. Sie haben einen kleinsten, einen größten und einen wirksamen Durchmesser. Die auf unterschiedliche Durchmesser bezogenen Abwicklungen haben unterschiedliche Länge. Je kürzer die Abwicklung, d.h. je kleiner der Bezugsdurchmesser, desto steiler und scharfkantiger sind alle Übergänge.

Zylinderkurven haben deshalb manchmal Unterschnitt auf dem inneren Kurvendurchmesser, aber durchweg runde Übergänge auf Wirk- und Außendurchmesser. Wenn Zylinderkurven auf dem Wirkdurchmesser unterschnittfrei sind, kann geringfügiger Unterschnitt auf dem kleinsten Flankendurchmesser meistens hingenommen werden. Problematisch ist es jedoch, so etwas im CAD auszutragen. Unsere Software OPTIMUS MOTUS erkennt Unterschnittbereiche und ersetzt sie beim Export von 3D-Daten automatisch durch Rundungen.
Wegen der Abhängigkeit der Kurven-Steigungen vom Bezugsdurchmesser werden Stege bei Zylinder-Stegkurven in der Regel dünner, je kleiner der Bezugsdurchmesser auf der Kurve ist. Es ist deshalb im Extremfall möglich, dass ein Kurvensteg auf Wirk- und Außendurchmesser ausreichend breit und tragfähig ist, während auf dem kleinsten Flankendurchmesser ein regelrechtes Loch entsteht.
In der Software OPTIMUS MOTUS werden die Kurvenflanken auf mehreren Bezugsdurchmessern exakt berechnet, so dass ein genaues 3D-Modell der Kurvenflanken bzw. des Rollenspurvolumens zur Verfügung steht, das sich auch für hochpräzise Bearbeitungen wie das Koordinatenschleifen eignet.
Koordinatensysteme
Um Zylinderkurven zu berechnen und CAD- und NC-Daten für Konstruktion und Fertigung abzuleiten, muss man sich auf entsprechende Koordinatensysteme beziehen. Diese können für Berechnung, CAD-Daten, NC-Metadaten und an der Werkzeugmaschine unterschiedlich sein, was in der Praxis leicht zu Fehlern und Mißverständnissen führt. Gerade bei der Aufbereitung von NC-Daten für konkrete Werkzeugmaschinen muss man höllisch aufpassen, dass vor allem die Achsrichtungen bei der Transformation der NC-Metadaten korrekt umgewandelt werden.
Bei der Berechnung von Zylinderkurven entstehen zunächst NC-Metadaten in einem festgelegten Koordinatensystem und in einem neutralen Format, die dann von Postprozessoren in maschinenspezifische Koordinatensysteme und Datenformate umgewandelt werden. Insgesamt haben wir im Laufe der Zeit etwa 200 Postprozessoren entwickelt, die jeweils Daten direkt für eine konkrete Werkzeugmaschine erzeugen. Ein solcher Postprozessor ist eine sehr sichere Art, NC-Daten für das Fräsen bzw. Schleifen von Zylinderkurven zu erzeugen. Daneben gibt es eine Reihe von Postprozessoren in neutralen bzw. weit verbreiteten Standardformaten.
Es spielt auch eine Rolle, mit welcher Seite die Kurve auf dem Rundtisch bzw. der Referenzfläche auf dem Teilapparat aufgespannt wird. Vertauscht man die Aufspannseite, müssen für alle drei programmierten Koordinaten die Vorzeichen gewechselt werden.
Für die NC-Metadaten verwenden wir folgendes Koordinatensystem:
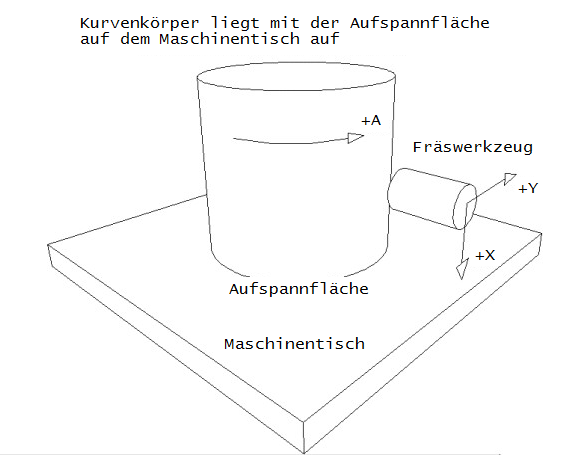
X = Kurvendrehachse, hauptsächliche Hubrichtung
Y = Mittenauswanderungsachse, senkrecht zu X, in der Bewegungsebene des Abtriebsgliedes
A = Kurvendrehwinkel bzw. Rundtischwinkel nach der Linke-Hand-Regel (wegen der kinematischen Umkehr bei der Berechnung)
Um die Metadaten korrekt für eine Werkzeugmaschine aufbereiten zu können, stellt man sich am besten mit der obigen Skizze vor die Maschine, lässt die drei Achsen für Hub, Mittenauswanderung und Rundtischdrehungen ins Plus laufen und notiert die beobachteten Verfahrrichtungen und Achsbezeichnungen auf der Skizze.
Beispiel: Man lässt das Werkzeug in Richtung Aufspannfläche fahren (bei unseren Metadaten +X) und beobachtet an der Maschine, dass dabei die Z-Achse ins Minus fährt (als Beispiel!). Also notiert man "-Z" auf der Skizze neben dem "+X" für die Metadaten. So ermittelt man empirisch an der Maschine - das ist nach unserer Erfahrung der sicherste Weg - die Transformationsregel "Metadaten +X wird umgerechnet in Werkzeugmaschine -Z".
Dies ist nur ein Beispiel! Bei Ihrer Maschine gelten möglicherweise andere Transformationsregeln.
Beim Export von CAD-Daten wird die Rundtischachse nicht benötigt, vielmehr stellt man die Kurvenbahnen in aller Regel als Punktfolge mit X/Y/Z-Koordinaten dar, die sich auf ein Kurvenkoordinatensystem beziehen.
Bei uns entspricht die X-Achse des Kurvenkoordinatensystems der Kurvendrehachse.
Die Y-Achse (senkrecht zu X) fällt zum Zeitpunkt phi=0 (Anfang Bewegungsplan) mit der Y-Achse der NC-Metadaten zusammen. Wenn die Kurve bzw. der Rundtisch sich drehen, bleibt die Y-Achse der NC-Metadaten relativ zur Umgebung fix, während die Y-Achse des Kurvenbauteils relativ zum Kurvenkörper fix bleibt.
Die Z-Achse wird nach der Rechte-Hand-Regel aus X und Y ermittelt: Z = X x Y. Z steht senkrecht zu X und Y.
Bei beiden Koordinatensystemen (für NC-Metadaten und für die CAD-Daten) liegt der Nullpunkt auf der Kurvendrehachse.
Herstellung
Für die Herstellung von Zylinderkurven legen wir die gleichen Genauigkeitsmaßstäbe an wie bei ebenen Kurven. Abschläge sind höchstens in dem Rahmen zulässig, in dem der Rundtisch zusätzliche Fehler hineinbringt. Insgesamt muß man bei Kurvenscheiben und bei Zylinderkurven in der Regel eine Bahngenauigkeit von 0.02mm fordern können.
Wenn die geforderten Genauigkeit einmal nicht umgesetzt werden konnten, ist der Grund dafür oft nicht leicht zu finden. In einem solchen Fall können wir mit unserer Erfahrung vielleicht helfen.
Zylinderkurven werden auf Werkzeugmaschinen mit Rundtisch hergestellt. Dabei werden gleichzeitig mindestens vier Achsen interpoliert. Der Rundtisch (bzw. ein Teilapparat) werden benötigt, um die Drehung der Kurve um ihre Achse abzubilden.
Bei der Herstellung einer feststehenden Kurve mit umlaufenden Abtrieben wendet man die "kinematische Umkehr an". Gedanklich überlagert man dem gesamten Kurvengetriebe eine Drehung in der Weise, dass die Abtriebslagerungen unbeweglich sind und statt dessen die Kurve dreht. Man wechselt also das Bezugssystem und betrachtet die Welt, als säße man auf der Stößelführung oder dem Schwinghebel-Lager.
Eine klassische, konservative, vorsichtige und teure Strategie ist, Zylinderkurven immer mit einem Werkzeug zu schlichten, dessen Durchmesser dem Rollendurchmesser entspricht. Das Werkzeug ersetzt dann im Eingriff mit der Kurve genau die Rolle. Wenn Sie bevorzugt größere Rollen mit z.B. 52mm, 80mm oder 110mm Durchmesser verwenden, wird das aber schnell kostspielig. Es wird ja dann immer ein Werkzeug mit exakt dem Nenndurchmesser benötigt. Schleift man das Werkzeug im Radius um 0.2mm nach, wird die Kurvenflanke im Bereich der Steigungen oft schon unzulässig verfälscht. Je nach Steigung sind dann Abweichungen von 0.1mm oder mehr locker drin.
Bei Nutkurven treten zudem zwei Probleme auf:
1.) eine Flanke wird im Gegenlauf und die andere im Gleichlauf hergestellt, mit entsprechendem Qualitätsverlust
2.) beim Startpunkt des Fräsvorgangs entsteht eine Kante, ein Versatz, der den Bewegungsablauf empfindlich stört
Leider bietet kaum eine CNC-Steuerung von Hause aus eine für Zylinderkurven verwendbare Werkzeugradius-Korrektur an.
Deshalb erzeugen wir NC-Daten für Zylinderkurvenflanken entweder für einen konkreten, vom Kunden bzw. Fertiger gewünschten Werkzeugdurchmesser (inklusive Verrechnung des Werkzeugradius), oder wir generieren NC-Programme, die die Werkzeugradius-Korrektur in Form einer Parameterprogrammierung enthalten.
Mit der Parameterprogrammierung kann der gewünschte Werkzeugdurchmesser noch an der CNC-Maschine vorgegeben werden.
Viele Zylinderkurven mit Rollendurchmesser 110mm können z.B. mit dem Werkzeugdurchmesser 20mm geschlichtet werden (oder 19.8mm, oder 19.5mm), ohne dass unzulässig hohe Abweichungen auftreten würden.
Dies reduziert die Werkzeug-Beschaffungskosten erheblich! Sie verwenden Standardwerkzeuge (z.B. Durchmesser 12mm, 16mm oder 20mm) und können diese auch noch nachgeschliffen einsetzen.
Wenn eine Zylinderkurvenflanke in einem Schnitt geschlichtet wird (wie das üblich ist), und wenn der Werkzeugdurchmesser dann kleiner ist als der Rollendurchmesser, werden in der Höhe der Kurvenflanke, also längs der Rollenachse, Abweichungen zwischen theoretischem Kurvenprofil und hergestellter Kurve auftreten.
In der Animation unter "Abwicklungsdarstellung" weiter oben stellt der rote Kreis ein Werkzeug dar. Gegenüber der Rollenmitte muss es immer senkrecht zur Kurvenbahn ausgelenkt werden, um das theoretische Kurvenprofil zu erreichen. Jedoch ist die entsprechende Auslenkrichtung abhängig vom Kurvenflankendurchmesser!
Wenn man eine Kurvenflanke in einem Schnitt schlichten will, also nicht "abzeilen", muss man sich für einen Bezugs-Kurvendurchmesser bzw. für jeweils eine Auslenkungsrichtung entscheiden. Auf allen anderen Kurvendurchmessern entstehen Abweichungen. Diese Abweichungen bewirken immer, dass zuviel Material stehen bleibt, dass Nuten also enger werden. Je größer die Steigung, je höher die Kurvenflanke und je größer die Differenz zwischen Rollen- und Werkzeugdurchmesser, desto größer die Abweichungen. Die Abweichungen wachsen etwa quadratisch mit der Differenz zum Bezugs-Kurvendurchmesser bei der NC-Aufbereitung. Bezieht man sich auf den Kurven-Wirkdurchmesser oder den mittleren Kurvenflankendurchmesser, entstehen relativ kleine Abweichungen.
Das "Abzeilen" der Kurvenflanke ist unattraktiv, weil der Fräsweg sehr lang wird und Längsriefen auf der Kurvenflanke entstehen, die das Tragbild der Rolle verschlechtern. Mehrere Schnitte mit einem zylindrischen Werkzeug sind ebenso unattraktiv.
Die Abweichungen, die entstehen, wenn man eine Zylinderkurve mit einem kleineren Werkzeug schlichtet, schätzen wir mit unserer Software OPTIMUS MOTUS ab. So sind wir sicher, dass wir mit unserem Wunsch-Werkzeugdurchmesser keine unzulässig hohen Profilabweichungen erzeugen. Oft sind diese Abweichungen sehr klein (kleiner 0.01mm), selbst wenn die Differenz zwischen Rollen- und Werkzeugdurchmesser sehr groß ist (z.B. 110mm zu 20mm).
Wir haben aber auch schon kritische Fälle mit einer rechnerischen Abweichung von 0.8mm gehabt. Dann muss man tatsächlich einen Werkzeugdurchmesser verwenden, der nahe am Rollendurchmesser liegt, oder die NC-Optimierung verwenden, die etwas weiter im Text erläutert wird.
Kurvenrollen sind oft ballig, so dass der Rollendurchmesser an den Kanten etwas kleiner ist als in der Mitte. Sehr oft verjüngt sich der Rollendurchmesser mit dem Abstand zur Rollenmitte schneller, als sich das entsprechende Aufmaß an der Kurve entwickelt. Das Tragbild zwischen Kurve und Rolle sieht dann z.B. so aus:
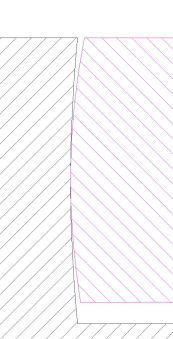
Kritisch wird es, wenn die Profilabweichung längs der Rollenachse schneller wächst, als es die Balligkeit der Rolle erlaubt. Dann läuft die Rolle immer nur mit einer Kante auf der Kurve, bei einer Nutkurve klemmt das Getriebe sogar.
Wenn man bei der Kurvenfertigung eine fünfte Achse zum Schwenken des Werkzeugs hinzuziehen kann (oft die B-Achse), kann dieser Freiheitsgrad genutzt werden, die Profilabweichungen zu verkleinern.
Unsere Software OPTIMUS MOTUS bietet die Option, NC-Daten vier- oder fünfachsig so nachzuoptimieren, dass die Profilabweichungen minimal werden. Bei einer Zylinderkurve und Verwendung von Standard-Werkzeugdurchmessern lassen sich die Profilabweichungen auf diese Weise gegenüber der vierachsigen Bearbeitung drastisch verringern.
Fasen
Beim Fräsen von Zylinderkurven entstehen zunächst scharfe Kanten zwischen Außenmantel und Kurvenflanken. Es ist verbreitet, diese Kanten mit einer Feile oder der Flex zu entgraten. Das ist aber sehr zeitaufwändig, und die von Hand entgrateten Kanten sehen auch nicht sehr schön aus. Mit speziellen NC-Programmen für kegelförmige Werkzeuge können diese Kanten programmgesteuert entgratet werden. Die räumliche Geometrie und damit die NC-Postprozessoren funktionieren dabei etwas anders als bei den Kurvenflanken.
Es entstehen saubere, gleichmäßig aussehende Fasen von definierter Breite, so dass die Kurven sofort hochwertiger aussehen. Außerdem muss niemand die Kante aufwändig von Hand bearbeiten, so dass auch die Fertigungskosten sinken.
CAD-Aufbereitung
Um zu einem guten CAD-Modell einer Zylinderkurve zu kommen, berechnen wir die Kurvenflanken auf 2 oder mehreren Referenzdurchmessern exakt und verwenden diese Raumkurven zum Austragen des "Rollenspurvolumens". Das Rollenspurvolumen ist das Volumen, das die Rolle insgesamt innerhalb des Kurvenkörpers einnimmt.
Zieht man das Rollenspurvolumen vom Kurvenrohling ab, erhält man ein Volumenmodell der Kurve.
Ein korrektes Volumenmodell der Kurve ist erforderlich, wenn davon mit einem NC-Programmiersystem CNC-Daten abgeleitet werden sollen.
Früher wurden die NC-Daten für die Zylinderkurven fast immer direkt bei der Kurvenberechnung erzeugt. Heute ist es sehr verbreitet, zunächst ein Volumenmodell der Kurve zu erstellen und dann davon NC-Daten abzuleiten.
Unsere Software OPTIMUS MOTUS stellt exakte Daten bereit, die für Austragungen geeignet sind, nach denen anschließend die Kurvenflanken gefräst werden.
Fehlermöglichkeiten
Erfahrene Kurvenberechner und Fertiger werden im Zusammenspiel in aller Regel ordentliche, gut laufende Zylinderkurvengetriebe herstellen.
Fehlt einem der Beteiligten jedoch die Erfahrung, passieren oft Fehler, die dazu führen, dass das Getriebe gar nicht oder nur schlecht läuft.
Bis zum Probelauf in der Maschine rechnet niemand mit Fehlern. Im Nachhinein den bzw. die Fehler zu finden, braucht viel Erfahrung und analytische Fähigkeiten.
Bei einer offenen Zylinderkurve, oft auch "Topfkurve" genannt, fallen Berechnungs-, Fertigungs- oder Montagefehler manchmal nicht unmittelbar auf, weil die Rolle immer irgendwie über die Kurvenflanke läuft. Dann stimmt aber das Tragbild zwischen Kurve und Rolle nicht, und es droht großer Verschleiß. Außerdem bewegt sich das Abtriebsglied nicht so, wie es bei der Berechnung vorgegeben wurde.
Bei formschlüssigen Kurven (Nutkurven oder Stegkurven) führen die meisten potenziellen Fehler nicht nur zu schlechten Tragbildern, sondern auch zum Klemmen des Getriebes, d.h. es läuft dann gar nicht. Das Klemmen könnte man einfach dadurch beseitigen, dass man die Kurvenflanken insgesamt um ein gewisses Maß zurücksetzt. Das führt jedoch im Betrieb zu Spiel und damit zu Stößen, weil die Profilfehler nicht überall gleich groß sind.
Spiel ist sehr schlecht für die Dynamik des Kurvengetriebes.
Es führt nur ein Weg zu guten Zylinderkurvengetrieben: korrekt rechnen, fertigen und montieren!
Für den Fall der Fälle hier eine Checkliste gängiger Fehlermöglichkeiten speziell bei Zylinderkurven:
- falsche Kinematik (z.B. Hebel eingebaut, aber mit Stößel gerechnet)
- mit falschen kinematischen Abmessungen gerechnet
- Exzenterbolzen eingesetzt, aber bei Berechnung nicht berücksichtigt
- Werkzeugdurchmesser zu klein für Steigung, Flankenhöhe und Rollendurchmesser
- Koordinaten nicht korrekt transformiert, insbesondere die Mittenauswanderungsachse
- keine korrekte Äquidistante gerechnet, sondern NC-Daten nur achsparallel verschoben
- Kurve falsch herum eingebaut (das sollte durch die Konstruktion ausgeschlossen werden!)
- räumliche Geometrie des Kontakts Rolle/Kurve nicht korrekt berücksichtigt
- falscher Austragungstyp im CAD verwendet
- Raumkurven für die Austragung im CAD nicht korrekt ermittelt
- Rundtischachse hat Umkehrspiel
- Zylindermantel-Abwicklungsfunktion der CNC-Steuerung verwendet
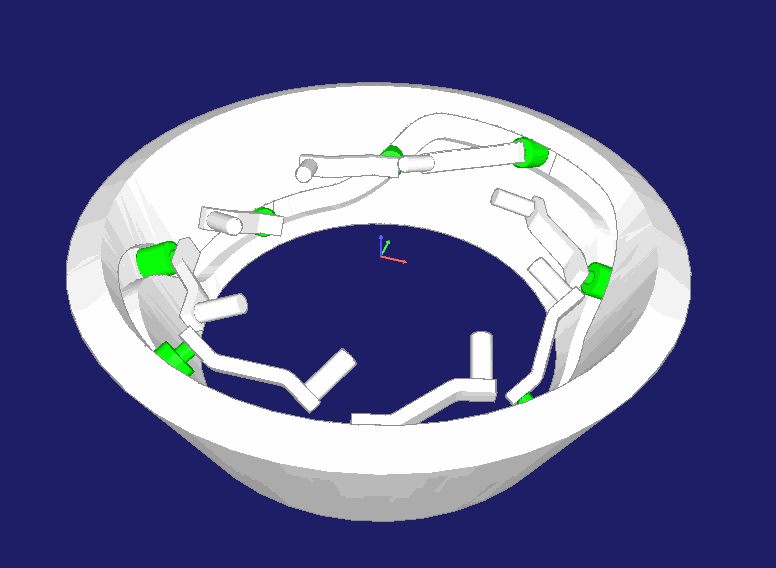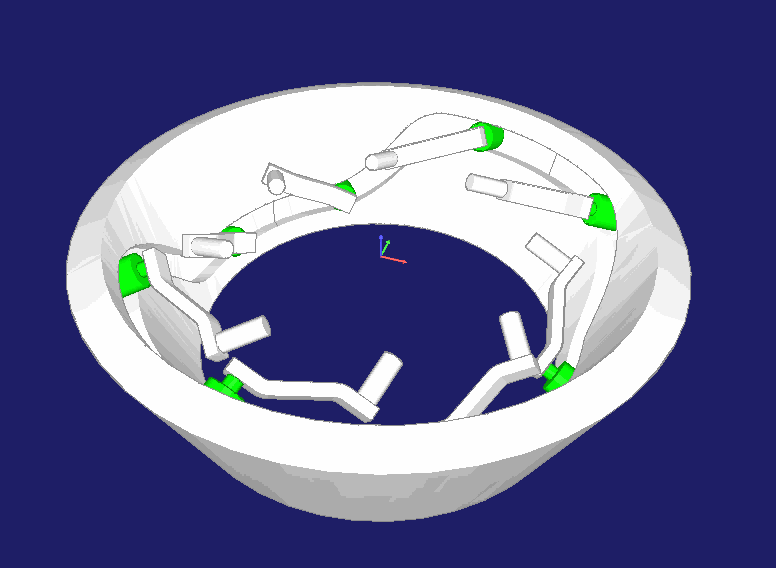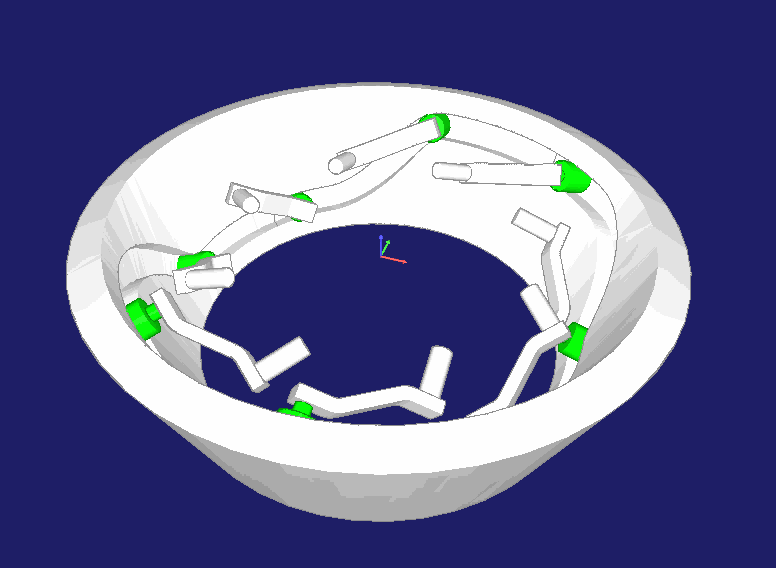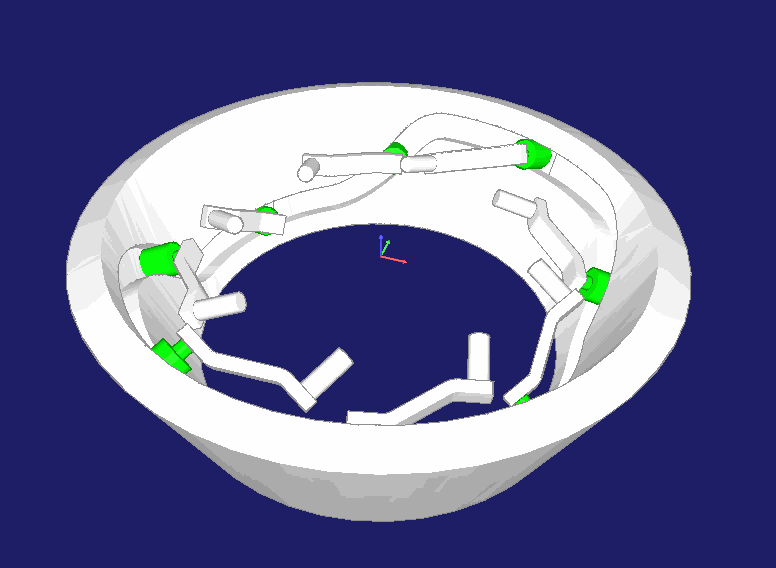
Spezielle Bauformen
Schließlich noch Bilder von speziellen Bauformen, die wir mit unserer Software berechnen können, und die mit Zylinderkurven verwandt sind:
Ein Abtriebs-Schlitten muss nicht unbedingt parallel zur Kurvendrehachse fahren:

Die Rolle von Abtrieb und Antrieb können auch umgekehrt werden. In der folgenden Animation wird der Kolben angetrieben, z.B. durch einen Pneumatikzylinder oder einen Pressenstößel, und die Drehung der Kurve wird für die Bewegungssteuerung verwendet.

Kurvenbahnen können auch auf der Innenseite eines Kegelrings kinematisch korrekt berechnet und hergestellt werden. Getriebe dieser Art werden beispielsweise in Maschinen verwendet, die Kabelummantelungen flechten:
zur Startseite von Nolte NC-Kurventechnik GmbH
Start Fachberichte Mechanismen Kinematik Kurvengetriebe Schrittgetriebe Fortbildung Servo/SPS Bewegungen Software Service Kurvenberechnung Impressum Datenschutz
Abwicklungsdarstellung Koordinatensysteme Herstellung Fasen CAD-Aufbereitung Fehlerquellen Spezielles
11/06/21
• Software OPTIMUS MOTUS ® /
DasNolte ®
• Berechnung von Kurven aller Art
• Performance-Optimierung
• Trainings und Beratung
• App- und Software-Entwicklung
• SPS-Bewegungsprogramme
Kurven, Mechanismen, Bewegungsdesign. Für schnellere Maschinen. Seit 1965.