Energetische Optimierung von Mechanismen
Energie zu sparen, den CO2-Ausstoß zu verringern und damit unseren gemeinsamen Lebensraum zu schützen, ist eines der wichtigsten Ziele der Menschheit. Das betrifft selbstverständlich auch den Maschinenbau.
Energie geht überall da verloren, wo sie transportiert wird, nämlich in Form von Reibung. Keine Maschinenkomponente hat einen Wirkungsgrad von 100 %.
Wenn Sie in einem Hochhaus zu Fuß ins 15. Stockwerk laufen und dann gleich wieder zurück ins Erdgeschoss, befindet sich Ihr Körper am Ende auf der gleichen Höhe wie am Anfang, hat also die gleiche potenzielle Energie inne wie zuvor. Scheinbar ist keine Energie verloren gegangen. Wenn Sie nur nicht so schwitzen würden ...
Eine Maschine "schwitzt" auch. Der zugeführte Strom erwärmt Kabel, Umrichter und den Motor, und die Wärme wird in die Umgebung abgeführt. Die Motoren treiben Getriebe, Spindeln, Riemen, Ketten, Räder, Federn, Hebel und Produkte an. Unter Last oder einfach kinematisch bedingt verformen sich Teile rhythmisch, werden regelrecht durchgeknetet, denn nichts ist absolut starr, und produzieren so auch Abwärme. Luft und Öl werden verwirbelt und sorgen für weitere Wärmeverluste. Der Maschine wird warm.
Nun unsere ganz simple Idee:
Je weniger Energie am Abtrieb umgesetzt wird, dort wo die Mechanik auf das Produkt einwirkt, desto weniger Energie muß von der Steckdose bis ins Werkzeug bzw. ins verarbeitete Produkt und wieder zurück transportiert werden.
Wir optimieren Bewegungssteuerungen auch daraufhin, dass möglichst wenig Energie transportiert wird!
Nebenbei spart das nicht nur Energie. Es macht Maschinen auch schneller, denn mechanischer Energietransport bei wechselnden Lasten geht mit Verformungen und so auch mit Schwingungen einher. Optimiert man den Energiefluss, so verbessert man auch die Performance, letztlich die Zykluszeit.
Energetische Optimierungen werden besonders für sehr schnell laufende Maschinen durchgeführt, der Performance und der Schwingungsfreiheit wegen.
Das ist eines unserer Lieblingsthemen, und wir beraten Sie gerne dabei!
Direkt zu ...
- Energiediagramm
- Antriebsmoment
- Leistungsbilanz
- Niedriger Energieumsatz
- Energieeffiziente Bewegungsgestaltung
- Reduziertes Massenträgheitsmoment
- Leistungsausgleich/Momentenausgleich
- Momentenausgleichskurven
- Federkompensatoren
- Trägheitskompensatoren
- Eigenbewegung
- Schwungrad
- Massenkraftausgleich, Gestellkraftausgleich
- Konstruktionshinweise
- Software
- Berechnung
- Seminar
zur Startseite von Nolte NC-Kurventechnik GmbH
> English version of this page
Energiediagramm
Das Energiediagramm in OPTIMUS MOTUS zeigt Verläufe von kinetischen und potenziellen Energien und von Leistungen im Gesamtmechanismus.
Es dient dazu, den Energiefluss im Mechanismus zu bewerten und Maßnahmen abzuleiten, um die Gesamtenergie im Mechanismus möglichst konstant zu halten.
Denn: je konstanter die Energie im Mechanismus, desto weniger Leistung muss der Antrieb umsetzen, und desto kleiner ist Antriebsmoment an der Kurvenwelle.
Antriebsmoment
Bei Kurvengetrieben und bei Servoantrieben ist das Antriebsmoment von besonderer Bedeutung.
Das maximale Moment muss kleiner sein als das maximal zulässige Moment im Antriebsstrang, das typischerweise durch Motor oder Getriebe gegeben ist, manchmal aber auch durch andere Komponenten. Das zulässige Maximalmoment ist in der Regel abhängig von der Drehzahl des Antriebs.
Damit der Motor nicht thermisch überlastet wird, muß der Effektivwert des Momentenverlaufs, das “Effektivmoment”, als quadratisches Mittel kleiner sein als das Nennmoment des Motors. Luft- oder Wasser-Kühlung erhöht das zulässige Dauermoment (Nennmoment) des Motors deutlich (Größenordnung: 30 %).
Werden von einem Antrieb mehrere Kurven angetrieben, so sollte das Summenmoment betrachtet und optimiert werden, also die Überlagerung aller Einzel-Momentenverläufe!
Das Zusammenspiel von Rückholfedern bei federbelasteten Kurven kann manchmal so optimiert werden, daß die Energie im Gesamtmechanismus ungefähr konstant gehalten wird. Dazu werden die Arbeitsrichtungen und die Parameter aller Rückholfedern in einer gemeinsamen Betrachtung optimiert. Das bewirkt letztlich, dass das Antriebsmoment an der Kurvenwelle erheblich sinkt.
Harmonisch gestaltete Summenmomentenverläufe an einer Kurvenwelle mit geringen Extremwerten vermeiden Schwingungen im Antriebsstrang.
Vorsichtig sollte man sein, wenn eine Kurvenwelle durch eine Kette angetrieben wird. Bei niedriger Zähnezahl eines beteiligten Kettenrades können Schwingungen durch den Polygoneffekt angeregt werden.
Speziell bei längeren Ketten ist deren Elastizität zu berücksichtigen, damit über die Wechselbelastungen keine Torsionsschwingungen an der Kurvenwelle auftreten, die über die Übertragungsfunktionen der Kurve auf die von den Kurven bewegten Werkzeug durchschlagen.
Besonders interessant ist die Abbremssimulation, die wir in unserer Software OPTIMUS MOTUS anbieten, um das Not-Stopp-Verhalten einer Kurvensteuerung zu untersuchen.
Für ein kinetostatisches Simulationsmodell erhalten Sie innerhalb weniger Sekunden durch eine übersichtliche Grafik eine genaue Information, welches Haltemoment die Bremse aufbringen muss, um die Kurvenwelle aus jeder Zwischenstellung heraus in definierter Zeit in den Stillstand zu bremsen. Genauso einfach lässt sich ermitteln, wie lange es maximal dauert, bis die Kurvenwelle zum Stillstand kommt, wenn das Haltemoment der Bremse bekannt ist.
Leistungsbilanz
Die Leistungsbilanz ist ein einfacher Ansatz, um das erforderliche Antriebsmoment für eine Kinematik zu ermitteln. Sie ist bei einem Mechanismus mit einem einzelnen durchlaufenden Antrieb mit der Antriebsfunktion psi(phi) anwendbar. Der Antrieb dient als Energiespender und als Rücknehmer überschüssiger Energie. phi ist ein Zeitparameter, z.B. unmittelbar die Zeit t in Sekunden oder ein gleichmäßig laufender Taktwinkel von 0 bis 360 Grad.
Die in einem Mechanismus gespeicherte Energie ist - über den Bewegungszyklus betrachtet - in der Regel nicht konstant. Der Mechanismus speichert Energie in den bewegten Massen in Form von potenzieller und kinetischer Energie. Federn speichern potenzielle Energie. Außerdem kann Energie im Verarbeitungsprozess an die Produkte oder in Form von Reibung an die Umgebung weitergegeben werden. Die in den Massen gespeicherte Energie ändert sich mit ihrer vertikalen Lage und mit ihrer Geschwindigkeit. Die in den Federn gespeicherte Energie variiert mit der Federlänge.
Der Trick ist nun: Bei der Leistungsbilanz kommt es nicht darauf an, welchen Weg die Energie im Mechanismus nimmt, d.h. wie der Mechanismus genau aufgebaut ist. Der Mechanismus kann als black box betrachtet werden. Man muss nur die Bewegungen der Energiespeicher und die Antriebsbewegung kennen, um ein Antriebsmoment zu berechnen.
In vielen praktischen Anwendungsfällen bewegt sich im Wesentlichen eine große Masse am Abtrieb des Mechanismus nach einem definierten Bewegungsdiagramm, und die Antriebsfunktion ist ebenfalls bekannt. Das muss dabei nicht eine lineare Funktion mit konstanter Geschwindigkeit sein. Der Antrieb sollte aber nicht zum Stillstand kommen, damit omega nicht 0 wird (siehe unten).
Zunächst berechnet man über dem Taktwinkel phi den Verlauf der Gesamtenergie W(phi) im Mechanismus.
Durch Ableitung nach der Zeit erhält man den Verlauf der Leistung P(phi), die vom Mechanismus umgesetzt wird und somit auch vom Antrieb umgesetzt werden muss:
P(phi) = dW(phi) / dt
Die Antriebsleistung Pan(phi) ist als
Pan(phi) = Man(phi) • omega(phi)
darstellbar. Dabei ist
omega(phi) = d(psi(phi)) / dt
Mit der Bilanz P(phi) = Pan(phi) kann das Antriebsmoment Man(phi) berechnet werden:
Man(phi) = P(phi) / omega(phi)
P = Leistung in W
Man = Antriebsmoment am Motor in Nm
Pan = Antriebsleistung in W
psi = Antriebswinkel in rad
omega = Antriebs-Winkelgeschwindigkeit in rad/s
Bei konstanter Kurvendrehzahl ist P ~ M bzw. M = P / omega = P / (pi•n/30) mit n = Drehzahl in U/min.
Niedriger Energieumsatz
Um Energie zu sparen, wird heute gerne vorgeschlagen, die Bremsenergie von Servoantrieben in den Frequenzumrichtern zurückzuspeisen, so dass sie nicht in Form von Wärme verloren geht. Das ist gut, aber auch hier fließen Ströme, die zu Abwärme führen. Die Energieausbeute durch Rückspeisung ist nicht sehr groß.
Unseres Erachtens wäre es klug, z.B. durch Leistungsausgleich schon die Mechanik so auszuführen, dass der Antrieb wenig Energie umsetzen muss. Wo keine Bremsenergie anfällt, muss man sich auch keine Gedanken um Bremswärme oder Rückspeisung machen!
Energieeffiziente Bewegungsgestaltung
Bewegungsdesign ist ein sehr kostengünstiges Mittel, um in Mechanismen Energie zu sparen.
Bei Kurven und Servoantrieben können die Bewegungen so gestaltet werden, dass insgesamt möglichst wenig Energie zwischen Antrieb und Mechanik ausgetauscht wird.
Beispielsweise durch ...
- Auswahl von Bewegungsgesetzen mit niedrigem dynamischen Momentenkennwert Cmdyn. Je kleiner der Kennwert, desto geringer der Energieumsatz.
Das bekannte Polynom 5. Grades hat einen Kennwert von Cmdyn=6.69. Die ebenfalls verbreitete Modifizierte Sinuslinie ist durch Cmdyn=5.46 gekennzeichnet.
Die von uns entwickelten Energiesparpolynome haben dagegen Kennwerte von Cmdyn=3.58 (ruckfrei) bzw. Cmdyn=2.70 (ruckbehaftet). - Kollisionsoptimierung, die die dynamischen Belastungen insgesamt minimiert und damit quasi automatisch auch den Energieumsatz.
- günstige Überlagerung von Leistungsanforderungen. Der Gesamtbewegungsablauf kann dahingehend optimiert werden, z.B. durch zeitliches Verschieben von Start- und Endpunkten und durch Auswahl von Bewegungsgesetzen, dass sich Leistungsabgabe und Leistungsrücknahme an einem Antrieb bestmöglich ausgleichen. Bei der Bewegungsoptimierung muss dazu stets das Summenmoment bzw. die Summen-Leistung betrachtet werden.
Reduziertes Massenträgheitsmoment
Bei Mechanismen ist das auf die Antriebswelle bezogene ("reduzierte") Massenträgheitsmoment in der Regel nicht konstant, sondern ändert sich mit dem Übersetzungsverhältnis zwischen Antrieb und Bewegung der Masse.
Es ist sehr wichtig, das bei der Auslegung der Antriebe zu berücksichtigen, denn sonst erhalten Sie schlichtweg falsche Ergebnisse. Bei falschen Ergebnissen wählen Sie zu große Antriebe (teuer!) oder zu kleine (Probleme bei der Inbetriebnahme, Diskussionen mit dem Kunden, noch teurer!).
Ein einfaches und sehr verbreitetes Beispiel für große Nichtlinearität ist die Schubkurbel, die wegen des Kniehebeleffekts (große Kräfte in den Endlagen) und der mechanisch genauen Einhaltung der Bewegungsendlagen sehr beliebt ist.
Allgemein läßt sich das reduzierte Massenträgheitsmoment Jred(phi) am Antrieb eines Mechanismus, das alle trägen Massen in ihrer Wirkung ersetzen soll, über folgende Beziehungen ermitteln:
Damit ist das Antriebsmoment Mkin auf Grund träger Massen:
In vielen schnellaufenden Mechanismen überwiegt das Antriebsmoment auf Grund träger Massen so deutlich, daß man andere Einflüsse bei der Optimierung vernachlässigen kann.
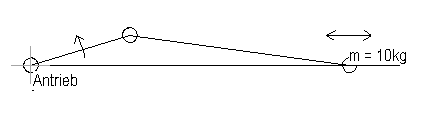
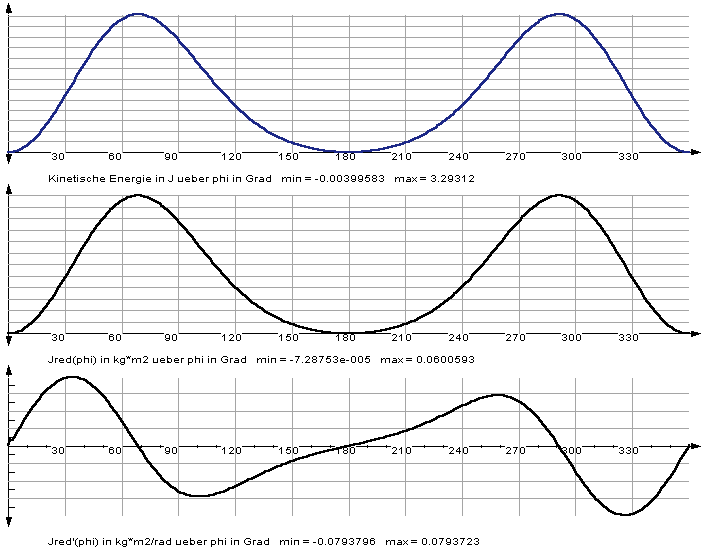
Beispiel: Schubkurbelgetriebe
Die Verläufe der kinetischen Energie Wkin, des reduzierten Massenträgheitsmoments Jred und der Ableitung J’red des reduzierten Massenträgheitsmoments nach phi:
Leistungsausgleich/Momentenausgleich
Mit dem Leistungsausgleich hält man die Antriebsleistung - und bei konstanter Antriebsdrehzahl auch das Antriebsmoment - eines Mechanismus möglichst konstant. Ohne Nutzkräfte und Reibung könnte das Antriebsmoment eines Mechanismus rechnerisch auf Null (!) reduziert werden.
Ziele:
- Antriebsenergie sparen
- Leistungsspitzen vermindern
- Momentenspitzen reduzieren
- Gleichförmigkeit verbessern
- Anregung der Antriebswelle zu Schwingungen vermindern
Mechanismen mit konstantem, kleinem Antriebsmoment sind sehr gut regelbar, verbrauchen wenig Energie und können ruhiger laufen.
Bei konstanter Antriebsdrehzahl ist Leistungsausgleich gleichbedeutend mit Antriebsmomentenausgleich.
Jred ist ein reduziertes (fiktives) Massenträgheitsmoment und speichert bei der Antriebsgeschwindigkeit dphi/dt die gleiche kinetische Energie wie alle tatsächlichen Mechanismenglieder.
Die häufigsten Maßnahmen zum Leistungsausgleich:
- Schwungrad: geringer Konstruktionsaufwand, geringere Schwankungen von Antriebsmoment und –drehzahl, höhere kinetische Antriebsenergie, Beschleunigungs- und Bremsarbeit, längere Anlauf- und Bremszeiten
- Ändern von Masseparametern (manuell durch Probieren oder rechnerisch durch numerische Optimierung)
- Angleichen der Antriebsbewegung an die Eigenbewegung
- Anpassen der Abtriebsbewegung an den Lastverlauf (Bewegungsgesetze optimieren)
- Federkompensatoren
- Momentenausgleichskurven mit Ausgleichsfeder
- Trägheitskompensatoren
- Momentenausgleichskurven mit Ausgleichsmasse
- Zusätzliche Mechanismen oder Servoantriebe
Je nachdem, welche Maßnahmen zum Leistungsausgleich verwendet werden, ist
- ein vollständiger Leistungsausgleich
- ein vollständiger Leistungsausgleich bei einer bestimmten Betriebsdrehzahl
- teilweiser Leistungsausgleich (Verringerung der Momentenschwankung) bei allen Drehzahlen
- ein teilweiser Leistungsausgleich bei Betriebsdrehzahl
erreichbar.
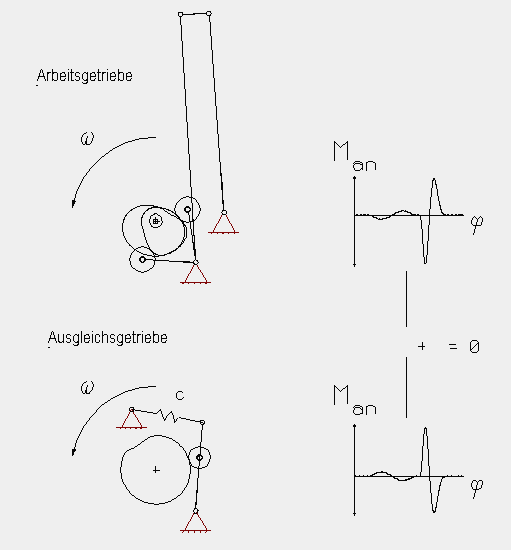
Momentenausgleich mit Kurven
Wenn die vom Mechanismus auf die Antriebswelle rückwirkenden Momente zu hoch sind, können Sie mit Hilfe einer Momenten- bzw. Leistungsausgleichskurve teilweise oder vollständig kompensiert werden. Die Momentenausgleichskurve sollte – bezogen auf den Kräfte- und Momentenfluss - so dicht an den Arbeitsmechanismen plaziert sein wie möglich.
Die Momentenausgleichskurve gibt zu jedem Zeitpunkt genau das Moment auf die Antriebswelle, das der Mechanismus vom Antrieb fordert. Wenn der Mechanismus Energie an den Antrieb zurückgibt, nimmt der Ausgleichsmechanismus diese direkt auf. Wenn der Lastausgleichsmechanismus dicht neben den Arbeitsmechanismen liegt, übt das Gesamtpaket aus Arbeits- und Ausgleichsmechanismen kein rückwirkendes Moment mehr auf den Antrieb aus.
Die Kontur der Momentenausgleichskurve wird aus dem Summenmomentenverlauf aller Arbeitskurven berechnet.
Grundsätzlich sind alle Kurven-Koppelgetriebe als Momentenausgleichskurven verwendbar. Es müssen jedoch immer Energiespeicher (Federn, Massen) im Mechanismus enthalten sein. Diese Energiespeicher fungieren als Quelle und Senke für die dynamischen Leistungs-Anforderungen (= Momenten-Anforderungen) der Arbeitsmechanismen.
Hinweis:
Momente auf Grund von Reibung oder Nutzlasten können nicht vollständig ausgeglichen werden, da die Energie, die in den Prozeß abgegeben bzw. als Wärme freigesetzt wird, nicht in den Antrieb zurückgespeist werden kann. Durch eine Momentenausgleichskurve können aber die unregelmäßigen Energieanforderungen des Prozesses bzw. die ungleichmäßigen Anforderungen an Reibungs-Energie gleichmäßig auf den gesamten Bewegungszyklus verteilt werden, so daß ein konstantes Restmoment am Antrieb auftritt.
Hinweis:
Für einen vollständigen Momentenausgleich über alle Drehzahlen hinweg werden mindestens zwei Ausgleichskurven benötigt:
- Eine Kurve mit einer Ausgleichsfeder. Diese gleicht alle Antriebsmomente durch statische Lasten aus (Federn, Prozeßkräfte, Gewicht).
- Eine Kurve mit einer Ausgleichsmasse. Diese gleicht alle dynamischen Antriebsmomente aus, die auf Grund träger Masse entstehen. Diese Kurve kann ggf. durch eine Druckregelung an der Ausgleichskurve für die statischen Lasten ersetzt werden.
Der Grund dafür liegt darin, daß die rückwirkenden Momente durch statische Lasten und Massenträgheit unterschiedlich von der Drehzahl abhängig sind:
- Statische Lasten sind unabhängig von der Antriebsdrehzahl.
- Trägheitslasten steigen proportional zum Quadrat der Drehzahl.
Oft ist es ausreichend, die Antriebsmomente bei einer bestimmten Betriebsdrehzahl auszugleichen. In diesem Fall reicht eine einzelne Ausgleichs-Kurve mit Ausgleichsfeder.
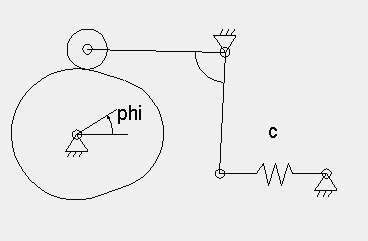
Häufig verwendete Kurvengetriebetypen für einen Momentenausgleichsmechanismus:
- Kurvenscheibe mit Schwinghebel und Ausgleichsfeder (siehe Bild) (vollständiger Ausgleich nur für eine Drehzahl möglich)
- Kurvenscheibe mit Schwinghebel und Druckzylinder (vollständiger Ausgleich für alle Drehzahlen mit drehzahlabhängiger Druckregelung möglich)
- Kurvenscheibe mit Stößel und Ausgleichsfeder (vollständiger Ausgleich nur für eine Drehzahl möglich)
- Kurvenscheibe mit Stößel und Druckzylinder (vollständiger Ausgleich für alle Drehzahlen mit drehzahlabhängiger Druckregelung möglich)
Je größer die Steifigkeit der Ausgleichs-Feder, desto kleiner wird der Hub auf der Ausgleichskurve.
Durch die Ausgleichskurve wird das Gesamtmoment (Summe von Antriebsmoment der Arbeitskurven und der Ausgleichskurven) zu Null:
Gerne berechnen wir Momentenausgleichskurven für Sie. Sprechen Sie uns an! Eine Mechanik mit Antriebsmoment 0 (bzw. nur Reibung) hätte doch was ...
Federkompensatoren
Angenommen, Sie haben eine beliebige Mechanik mit einem Antriebsmomentenverlauf Man(phi), und Sie wollen dieses Antriebsmoment mit Hilfe einer Feder als Energiepuffer kompensieren, dann kann der Verlauf der Federlänge über dem Antriebswinkel berechnet werden.
Dabei ist es ganz egal, wie der Mechanismus funktioniert, der das Arbeitsmoment Man(phi) fordert, und auch ganz egal, wie das Momentenausgleichsgetriebe aufgebaut ist!
Vorteile von Federkompensatoren:
- vollständiger Ausgleich der potentiellen Energie bei allen Drehzahlen möglich
- vollständiger Ausgleich der kinetischen Energie für eine Betriebsdrehzahl möglich
- teilweiser Ausgleich oft mit geringem Aufwand möglich
Nachteile von Federkompensatoren:
- Gefahr von Eigenschwingungen der Ausgleichsfedern
- Ausgleich von Trägheitslasten nur für eine Auslegungsdrehzahl möglich
Trägheitskompensatoren
Bei einem gleichmäßig angetriebenen Mechanismus kann das auf Grund träger Massen hervorgerufene Antriebsmoment kompensiert werden, indem an die Antriebswelle ein zusätzlicher Ausgleichsmechanismus angekoppelt wird, der eine Schwungscheibe mit Massenträgheitsmoment Jausgleich mit einer Funktion psi(phi) bewegt.
Vorteile von Trägheitskompensatoren:
- vollständiger Ausgleich der kinetischen Energie für beliebige, aber konstante Drehzahlen möglich
Nachteile von Trägheitskompensatoren:
- hoher konstruktiver Aufwand und erhöhter Platzbedarf
- erhöhte Gestell- und Gelenkkräfte
Eigenbewegung
Bei einem sich selbst überlassenen Mechanismus stellt sich eine sogenannte “Eigenbewegung” ein.
Diese Bewegung würde entstehen, wenn man den Antrieb plötzlich auskuppelte. Am Antrieb wird dann kein Moment mehr eingeleitet. Im Allgemeinen ist die Eigenbewegung ungleichmäßig.
Wenn man nun den Mechanismus von vornherein mit der Antriebsfunktion betreibt, die der Eigenbewegung entspricht, so braucht der Antrieb dauerhaft kein Moment aufzubringen, außer zur Überwindung von Reibung und Nutzkräften.
Die erforderliche ungleichmäßige Antriebsbewegung kann exakt über Kurven-Schrittgetriebe, Unrundräder, Servoantriebe oder näherungsweise über Koppelmechanismen eingeleitet werden.
Bei annähernd konstanter potentieller Energie:
Beispiel Schubkurbelgetriebe:
Antriebsmoment bei gleichmäßigem Antrieb an der Kurbel (links) und bewegter Masse am Schlitten (Anlenkpunkt rechts):
Antriebsfunktion für Kurbel-Antriebmoment Man = 0, d.h. wenn die Kurbel mit Hilfe eines Servoantriebs, eines Unrundräderpaars, eines Schrittgetriebes oder näherungsweise eines Koppelgetriebes so bewegt wird, muss nur das Reibmoment aufgebracht werden:
Schwungrad
Schwungräder werden in mechanischen Getrieben mit konstanter Antriebsdrehzahl eingesetzt, um die Schwankungen der Antriebswinkelgeschwindigkeit und damit des momentanen Motorantriebsmoments klein zu halten. Sie sind heute nur noch im Ausnahmefall anzutreffen.
In Verbindung mit geregelten Antrieben (Servoantrieben) ergeben sie keinen Sinn.
Bei vernachlässigbarer Schwankung des reduzierten Massenträgheitsmoments kann das Schwungrad für die Nutz- und Reibmomente ausgelegt werden:
W* = Arbeit aus Nutzlasten und Reibung für einen Bewegungszyklus
Vorteile des Schwungrades:
- geringer Konstruktionsaufwand
- geringere Schwankungen von Antriebsmoment und –drehzahl
Nachteile des Schwungrades:
- höhere kinetische Antriebsenergie, also höhere Beschleunigungs- und Bremsarbeit
- längere Anlauf- und Bremszeiten
Massenkraftausgleich, Gestellkraftausgleich
Maschinen geraten bei höheren Taktzahlen gerne in ihrer Aufstellung insgesamt in Schwingungen. Sie schütteln sich quasi.
Das gleiche gilt für weich aufgehängte Baugruppen in einem festen Gestell, z.B. schwere auskragende Komponenten.
Dabei handelt es sich um Eigenschwingungen, die durch die Kombination großer, hoch beschleunigte Massen und einer leichten, weichen Gestellkonstruktion hervorgerufen werden.
Früher - vor mehr als 40 Jahren - wurden Maschinen teilweise nach Gewicht bezahlt. Je schwerer die Maschine, desto höher der Preis. Das Gestell - und auch alle anderen Teile - wurden gerne sehr massiv ausgeführt. Die Schwingungsanregung im Gestell wird so im Keim erstickt. Diese Zeit ist vorbei, heute baut man leichter, mit weniger Material, und damit elastischer und potenziell schwingungsanfälliger. Werden Massen beschleunigt, reagiert das Gestell eher mit Verwindung.
Leider lassen sich die bewegten Massen nicht beliebig verringern, und die Taktzahl soll generell immer weiter steigen. Die Anregung des Gestells durch Massenkräfte kann zwar durch Bewegungsdesign verringert werden, aber manchmal bleibt die Restanregung so groß, dass weitere Maßnahmen erforderlich sind.
Dann versucht man, die Anregung des Gestells durch Kräfte und Kippmomente mit Hilfe von Ausgleichsmassen zu kompensieren.
Diese Ausgleichsmassen werden entweder in Form von Zusatzmassen oder Aussparungen auf die bestehenden Getriebeglieder aufgebracht, oder es werden zusätzliche Kurven- oder Koppelgetriebe eingebracht, um die Gestellanregung der Arbeitsmechanismen exakt oder näherungsweise auszugleichen.
Dies wird "Massenkraftausgleich" oder "Gestellkraftausgleich" genannt.
Prinzipiell ist das oft ziemlich einfach:
Für jeden Arbeitsmechanismus baut man eine Kopie um 180 Grad gedreht und so versetzt hinzu, dass die Massenschwerpunkte auf der gleichen Wirklinie laufen - fertig. Bewegt sich eine Masse m im Arbeitsmechanismus in +X, so bewegt sich die Ausgleichsmasse automatisch in gleicher Weise in -X. Beide Massen gleichen sich dann in ihrer Wirkung aus, und es entstehen keine Kippmomente.
Das Problem ist, dass dieser Ansatz sehr viel Bauraum erfordert, oft dort, wo er nicht zur Verfügung steht, und dass das natürlich sehr teuer ist.
Es geht aber auch einfacher, indem man versucht, Gegenmassen direkt an den bewegten Teilen des Arbeitsmechanismus anzubringen.
Die eigentliche Kunst ist, einen ausreichend effektiven Gestellkraftausgleich mit möglichst einfachen und kostengünstigen Maßnahmen zu erreichen.
Dabei unterstützen wir Sie gerne mit unserer Erfahrung und unserer Software OPTIMUS MOTUS.
Für den Gestellkraftausgleich nutzen wir spezielle numerische Optimierungsalgorithmen.
Die Ausgleichsmassen benötigen natürlich auch Energie und vergrößern das erforderliche Antriebsmoment. Wenn das Antriebsmoment durch die Ausgleichsmassen zu groß werden sollte, kann zusätzlich ein Antriebsmomentenausgleich durchgeführt werden, und zwar so, dass keine zusätzlichen Gestellkräfte entstehen.
Durch eine Kombination von Massenkraftausgleich und Momentenausgleich kann man einen theoretisch perfekt ausgependelten Mechanismus erreichen, der keine dynamischen Kräfte und Kippmomente in die Maschinenaufstellung einträgt und der lediglich ein kleines konstantes Antriebsmoment benötigt, um die Reibleistung aufzubringen.
Konstruktionshinweise
In der Praxis haben sich folgende allgemeine Tipps bewährt, um Energie sparende Bewegungssteuerungen auszulegen:
- Mechanik vor Elektrik vor Pneumatik
- von Mindestforderungen des Bewegungsverlaufs an der Wirkstelle ausgehen, nicht ohne Grund mehr fordern
- nur das technologisch Notwendige fordern, große Toleranzbereiche zulassen
- jeweils die kleinste Masse von Werkstück und Werkzeug bewegen
- Rückholfedern so anordnen, daß sie ihre Energiezuflüsse und Energieabflüsse gegenseitig optimal ausgleichen
- Eigenformen so verändern, daß sich die Arbeit verschiedener Erregerkräfte gegenseitig vermindert oder aufhebt
- Massen an Stellen verkleinern, an denen große Geschwindigkeiten auftreten
- Dämpfer vermeiden
- Servoantriebsdrehzahl nicht voll ausnutzen, oft ist ca. 1/3 des Maximums optimal
Mehr dazu erfahren Sie in unseren Seminaren!
zur Startseite von Nolte NC-Kurventechnik GmbH
Start Fachberichte Mechanismen Kinematik Kurvengetriebe Schrittgetriebe Bewegungsdesign Fortbildung Software Service Kurvenberechnung Impressum Datenschutz
Energiediagramm Moment Leistung Energiesparbewegung Trägheitsmoment Leistungsausgleich Eigenbewegung Schwungrad Gestellkraftausgleich Tipps+Tricks
11/06/21
• Software OPTIMUS MOTUS ® /
DasNolte ®
• Berechnung von Kurven aller Art
• Performance-Optimierung
• Trainings und Beratung
• App- und Software-Entwicklung
• SPS-Bewegungsprogramme
Kurven, Mechanismen, Bewegungsdesign. Für schnellere Maschinen. Seit 1965.