Globoidschaltkurven, Globoidkurven-Schrittgetriebe
Globoidkurven-Schrittgetriebe bzw. Globoidschaltkurven sind eine spezielle Anwendung der Globoidkurven und eine spezielle Form von Schrittgetrieben.
Globoidkurven-Schrittgetriebe sind sehr kompakt und steif, und die Schrittbewegung ist über harmonische, ruckfreie Bewegungsgesetze in weiten Grenzen frei gestaltbar. Durch Einstellung des Achsabstands ist das Getriebespiel optimierbar.
Globoidkurven-Schrittgetriebe sind sehr leistungsfähig und erreichen eine hohe Performance.
Deshalb sind sie in der Praxis sehr beliebt.
Bei spezieller Bewegungsgestaltung kann der gleiche Getriebetyp auch für andere Anwendungen zum Einsatz kommen, z.B. für Werkzeugwechselsysteme, als Vorschaltgetriebe für das Erreichen von Synchronlauf oder zur energetischen Optimierung.
Unsere Software OPTIMUS MOTUS enthält leistungsfähige und in der Praxis bewährte Bausteine, um Globoidkurven-Getriebe auszulegen, zu berechnen, zu simulieren und NC- und Fertigungsdaten zu erzeugen.
Bauen Sie auf unsere Erfahrung mit Globoidkurven-Schrittgetrieben!
Direkt zu ...
- Varianten
- Auslegung
- Spreizen
- Freischneiden
- Ausrundung
- Fasen
- Gangverkettung
- NC-Optimierung
- Berechnung
- Software
Zur Startseite von Nolte NC-Kurventechnik GmbH
> English version of this page
Varianten
Globoidkurven-Schrittgetriebe treten in verschiedenen Ausführungen auf:
Nut/Steg in der Mitte
Ein "normales" Schrittgetriebe enthält Rasten im Bewegungsablauf. Der Rollenstern durchläuft einen Schritt und verharrt dann eine gewisse Zeit in Ruhe. Ein Unterscheidungsmerkmal bei Globoidkurven-Schrittgetrieben besteht darin, wo die Rollen in der Rastphase liegen. Theoretisch kann der Rollenstern in jeder Winkellage relativ zur Kurve seine Rastposition einnehmen. Die Regel ist jedoch, dass die Rollen dann symmetrisch angeordnet sind.
Eine Möglichkeit dafür ist, den Rastbereich der Kurvennut mittig zu legen, wie in dieser Animation:
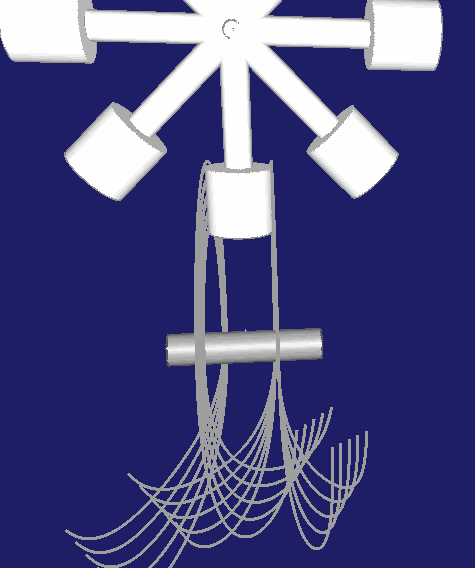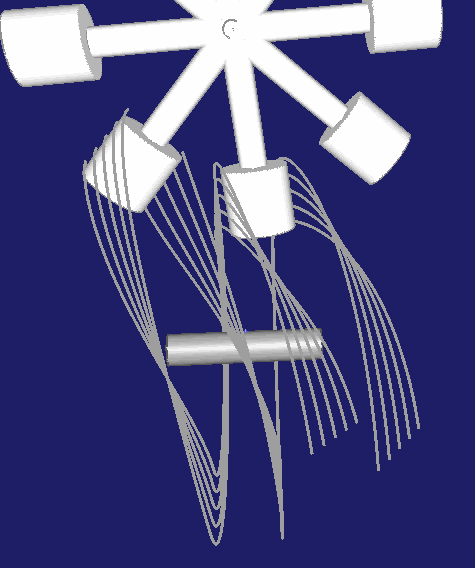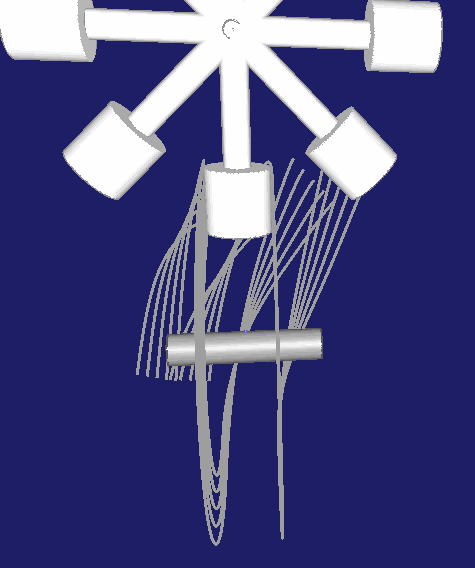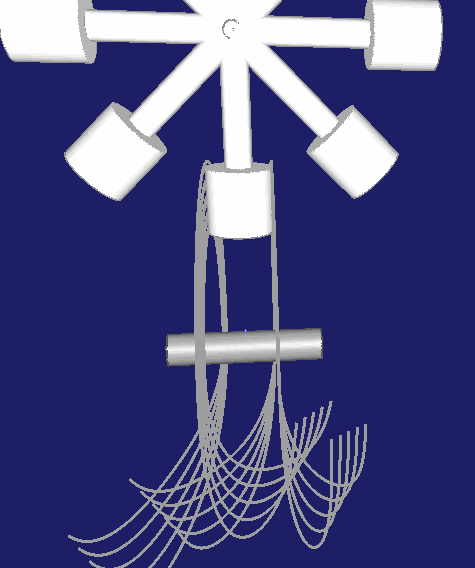
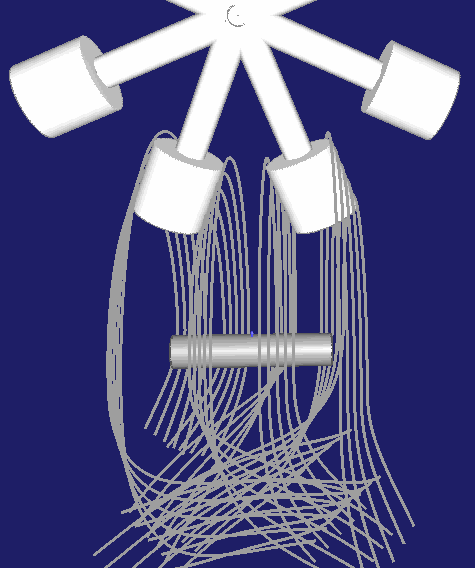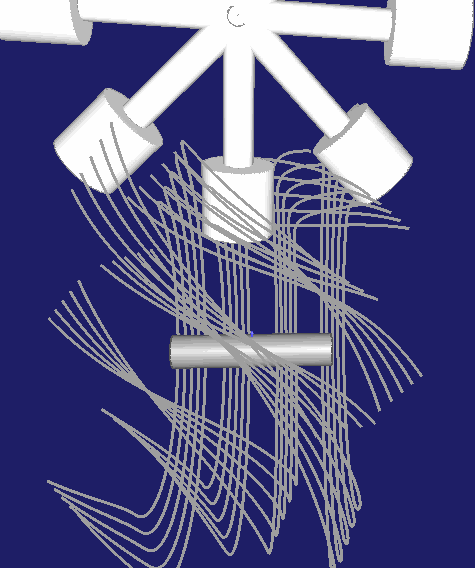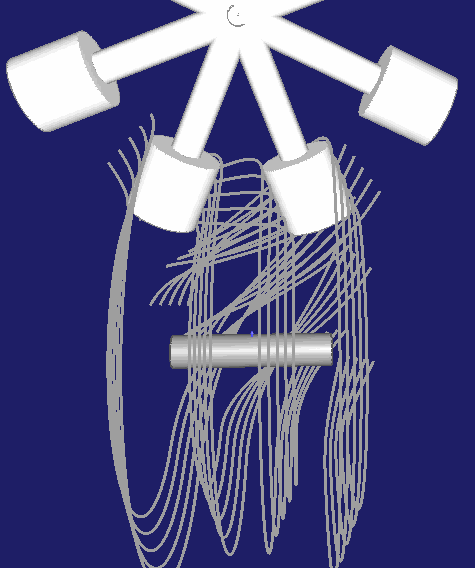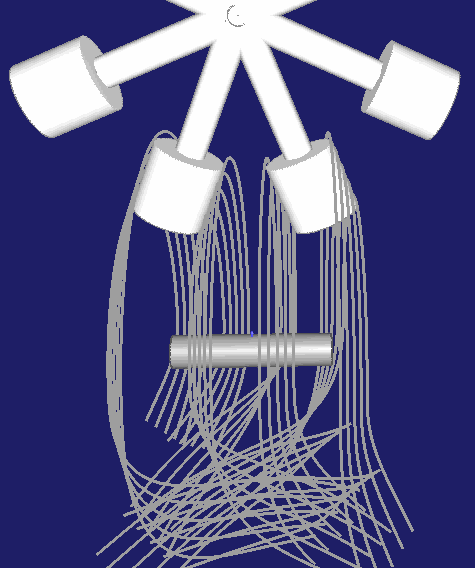
Wesentlich häufiger anzutreffen ist aber die Anordnung, in der der Rast-Steg zwischen zwei Rollen mittig gelegt wird, wie hier:
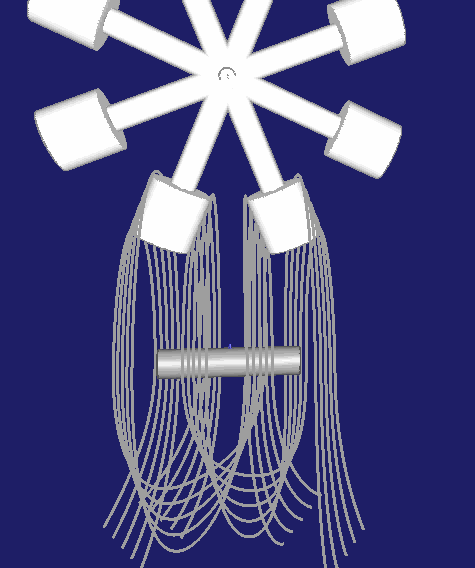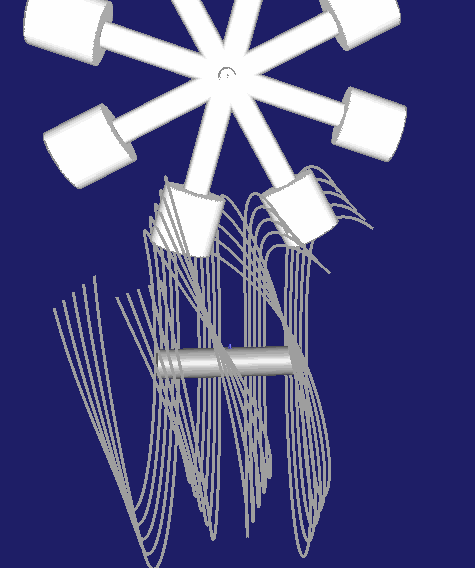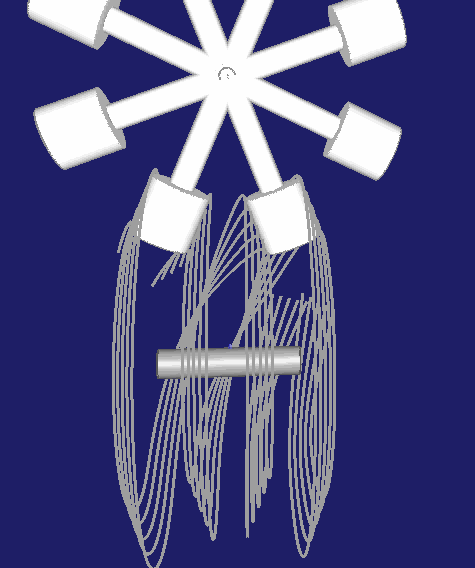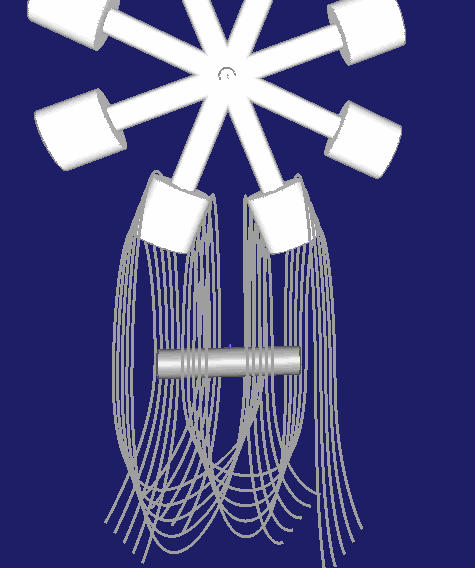
Der Vorteil bei dieser zweiten Anordnung besteht darin, dass das Kurvengetriebe-Spiel über den Achsabstand zwischen Kurvenwelle und Rollenstern-Drehachse eingestellt werden kann.
Eine wesentliche Aufgabe des Schrittgetriebes ist, den Rollenstern mit dem Drehteller in der Rast sicher zu fixieren, damit die Produkte auf dem Drehteller reproduzierbar bearbeitet werden können. Während der Schaltphase würde großes Spiel zu Stößen und damit zu Verschleiß führen. Optimal ist es häufig sogar, die Rollen mit der Kurve über den Achsabstand geringfügig zu verspannen.
Diese Spiel-Einstellung über den Achsabstand wird dadurch möglich, dass die Rollenachse und damit die Kontaktlinie zwischen Rolle und Kurve nicht senkrecht zur Kurvendrehachse liegt. Verändert man den Abstand zwischen Kurvendrehachse und Rollenstern-Drehpunkt, so bewegen sich auch die Rollen von der Kurvenflanke weg oder darauf zu.
Gänge
Ein weiteres Unterscheidungsmerkmal bei den Standardbauformen ist die Gängigkeit, also wieviele Kurvennuten nebeneinander benötigt werden. Die Gängigkeit entspricht der Anzahl Teilungen, um die sich der Rollenstern während einer Schaltung weiterdreht.
Die vorangegangenen beiden Animationen zeigen Schrittgetriebe mit jeweils einem Gang.
Hier eine Darstellung für ein zweigängiges Globoidkurven-Schrittgetriebe:
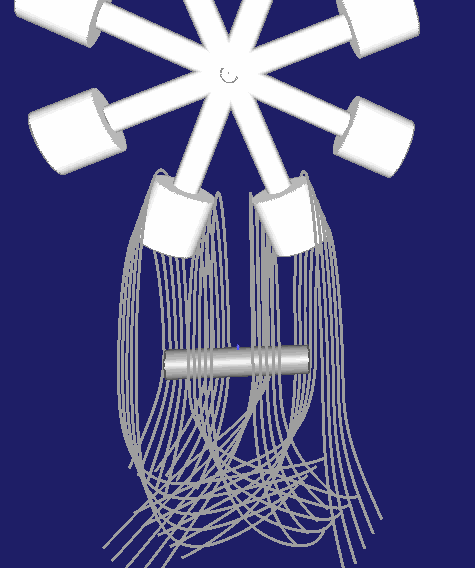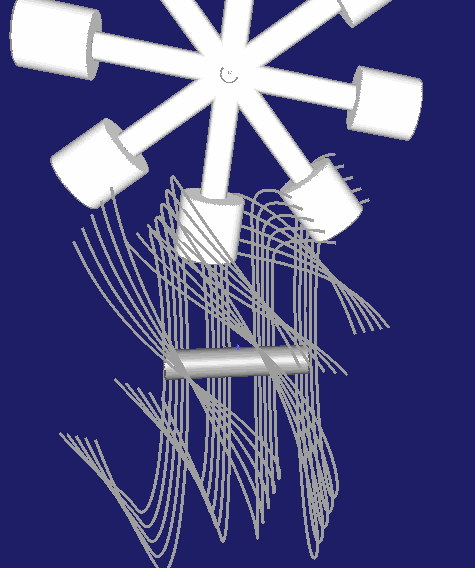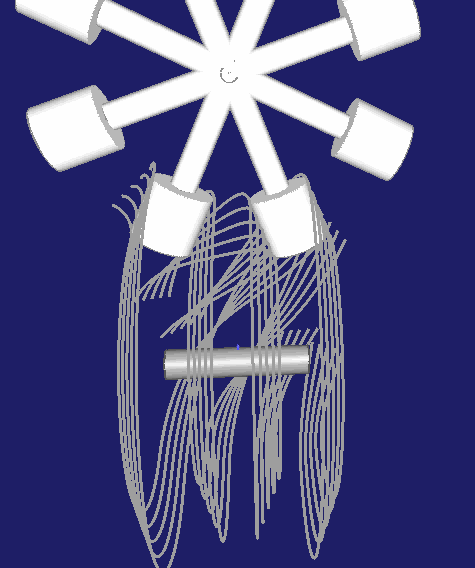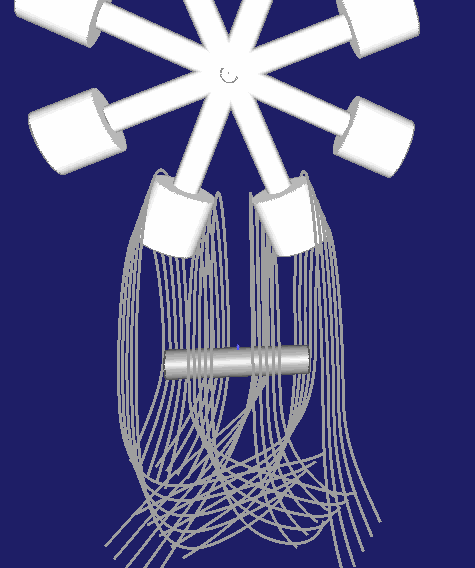
Schließlich noch eine Darstellung für eine dreigängige Globoidschaltkurve:
Schritt/Pilgerschritt/Durchlauf
Das "normale" Globoidkurven-Schrittgetriebe erzeugt aus einer kontinuierlichen Antriebsdrehbewegung eine schrittweise Abtriebs-Drehbewegung, also Schaltung und Stillstand im Wechsel. Ein spezieller Vorteil der Globoidkurven-Schrittgetriebe beispielsweise gegenüber den Parallelkurven-Schrittgetrieben ist, dass die Abtriebsdrehung auch in gleichem Maße rückwärts laufen kann.
So ist bei einem Globoidkurven-Getriebe auch eine oszillierende Abtriebsbewegung möglich, auch mit großem Abtriebs-Drehwinkel wie in folgender Animation:
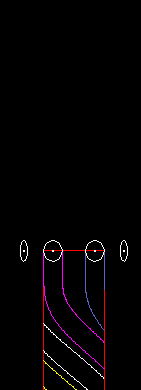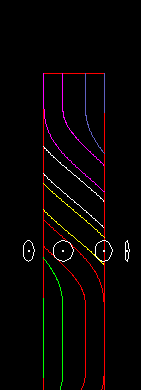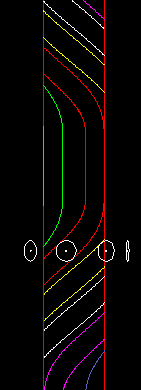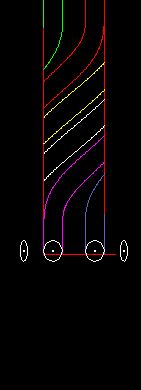
Kurven-”Schrittgetriebe” mit oszillierendem Abtrieb werden oft Pendelgetriebe genannt.
Denkbar sind auch Pilgerschrittbewegungen, also im Prinzip durchlaufende Drehungen, aber mit Rückwärtsschritten. Kurven dieser Art sind für Werkzeugwechsel-Einrichtungen im Gebrauch:

Weiterhin sind Globoidkurvengetriebe mit einer konstanten Übersetzung zwischen Antrieb und Abtrieb verbreitet. In einer Getriebestufe sind damit relativ große Übersetzungsverhältnisse möglich.
Das kinematische Konzept des Globoidkurvengetriebes lässt viel Freiraum bei der Gestaltung der Abtriebsbewegungen. Vorwärts und rückwärts sind sehr große Abtriebsbewegungen möglich.
Neben den Schrittbewegungen, den oszillierenden Bewegungen, den konstanten Übersetzungsverhältnissen und den Pilgerschrittbewegungen sind auch ganz allgemeine Abtriebsbewegungen ohne Stillstand möglich. Über ein Globoidkurvenschrittgetriebe könnte z.B. die Antriebsbewegung eines Koppelgetriebes so gestaltet werden, dass am Abtrieb des Koppelgetriebes ein bestimmtes Bewegungsgesetz oder eine konstante Geschwindigkeit herauskommt.
Unsere Software OPTIMUS MOTUS unterstützt alle diese Gestaltungsformen!
Sonderformen
Globoidkurven-Schrittgetriebe können wir noch weiter modifizieren und mit unserer Software berechnen, z.B. mit
- Kröpfung/Schrägstellung der Rollen auf dem Rollenstern
- Unregelmäßiger Rollenteilung bei mehrgängigen Kurven
- Einbringen der Nuten auf der Innenseite eines Kurvenrings statt von außen auf einen Kurvenmantel
- Kippung der Rollensternebene gegenüber der Kurvendrehachse
- Verwendung kegelförmiger oder extrem balliger Rollen
Auslegung
Im Vertrieb und bei der Projektierung von Schrittgetrieben wird eine schnelle Aussage benötigt, ob ein ins Auge gefasstes Globoidkurven-Schrittgetriebe mit einer bestimmten Last und bei der vorgegebenen Taktzahl hält, und welche Lebensdauer es voraussichtlich erreichen wird.
Genauso interessant ist, welche Getriebegröße für die geforderte Lebensdauer bei gegebener Last und gegebener Taktzahl erforderlich ist, bzw. ob ein Schrittgetriebe für die vom Kunden vorgegebenen Auslegungsparameter überhaupt lieferbar ist.
Der Anwender bzw. Kunde will einfach wissen, ob er für seine Transportanwendung ein geeignetes Schrittgetriebe bekommen kann, und wie teuer es dann ist.
Für diese Fragen gibt es in unserer Software OPTIMUS MOTUS ein spezielles Auslegungsmodul für Kurven-Schrittgetriebe.
Diese Software nutzen wir auch für Dienstleistungsberechnungen.
In eine Dialogbox tragen Sie die wichtigsten Eckdaten für die Kurvenberechnung ein, z.B. Achsabstand, Kurvenbreite, Rollensternradius, Rollenanzahl, Rollendurchmesser, Rollenballigkeit, dynamische Tragzahl der Rolle, Schrittwinkel, Schaltwinkel, Flankenhöhe, Laufhöhe, Drehteller-Massenträgheitsmoment, Taktzahl.
OPTIMUS MOTUS berechnet das Getriebe und bewertet kinematisch und dynamisch, ob das Getriebe lauffähig ist und welche nominelle Lebensdauer die Rollen und die Kurve erreichen können. Dabei wird auch berücksichtigt, dass eventuell mehrere Rollen im Eingriff sich die Belastung teilen!
Insbesondere werden folgende Werte ermittelt:
Überdeckungsweg
Mindest-Lauflänge, über die mehrere Kurvenflanken im Eingriff sind. Der Überdeckungsweg sollte größer als 0 sein, sonst kann die Kurve den Rollenstern nicht vollständig fixieren. Der Drehteller könnte sich dann frei bewegen.
Stegdicke
Kleinste Breite der Stege zwischen den Kurvennuten oben, in der Flankenmitte und im Nutgrund. Sind die Stege zu dünn, können sie nicht tragen.
Übertragungswinkel
Der minimale Übertragungswinkel ist ein Maß für die Steigung der Kurvenbahn im Durchlauf. Theoretisch ist 90 Grad der optimale Wert, aber nur bei Schrittwinkel 0 Grad erreichbar, als Auslegungsziel also nicht anzustreben. Den allgemeinen Empfehlungen folgend, ist 45 Grad ein guter, 60 Grad ein sehr guter Wert für den minimalen Übertragungswinkel. Letztlich hängt die Baugröße des Getriebes davon ab, welchen minimalen Übertragungswinkel man zulassen will.
Profilkrümmungsradius
Der minimale Profilkrümmungsradius für die konvexen Kurvenprofilbereiche wird am Außenrand der Kurvenflanke, in der Mitte und im Nutgrund ermittelt. Theoretische Werte unter 0 mm deuten auf Unterschnitt hin. Die theoretische Kurvenflanke hinterschneidet sich dort selbst. Wenn in Höhe des Kontaktpunkts zwischen Rolle und Kurve ein kleiner positiver Profilkrümmungsradius erreicht wird, ist die Kurvenauslegung in der Regel akzeptabel. Der kleinste Krümmungsradius wird durch etliche Auslegungsparameter beeinflusst.
Die Software OPTIMUS MOTUS verrundet die 3D-Daten in den Unterschnittbereichen automatisch, damit die Rollenspurvolumen (der Raum einer Kurvennut) im CAD trotz Unterschnitts ausgetragen werden können.
Maximal auftretende Rollenkraft
Die größte Kontaktkraft zwischen Rolle und Kurve.
Maximale Antriebsleistung
Der Maximalwert der geforderten Antriebsleistung in kW.
Rollenlebensdauer
Besonders interessant für die Projektierung ist die ermittelte nominelle Rollenlebensdauer in Stunden. Das ist die Lebensdauer, die statistisch gesehen von 90 % aller Lager bei den angenommenen Belastungen und Taktzeiten erreicht wird, ohne Berücksichtigung von Betriebsfaktoren. Wenn viele Rollen auf einem Rollenstern sitzen, so fällt der gesamte Rollenstern aber schon mit der ersten beschädigten Rolle aus, und es ist viel wahrscheinlicher, dass irgendeine von N Rollen ausfällt als eine ganz spezielle, vorher ausgewählte Rolle. Deshalb wird auch eine nominelle Rollenslebensdauer für den gesamten Rollenstern berechnet.
Kurvenlebensdauer
Typisch für gehärtete Kurvenflanken sind Härtegrade von 60 HRC oder 62 HRC. Über die maximale Hertzsche Pressung, die für den angegebenen Balligkeitsradius berechnet wird, schätzt unsere Software die erreichbare Lebensdauer der Kurvenflanke in Bezug auf Pittingbildung ab.
Maximale Abtriebsgeschwindigkeit
Die maximale Winkelgeschwindigkeit am Rollenstern während der Schaltung.
Maximale Abtriebsbeschleunigung
Die maximale Winkelbeschleunigung am Rollenstern während der Schaltung.
Darüber hinaus gibt das Programm Abschätzungen ab, mit welcher maximalen statischen Last, mit welchem maximalen Massenträgheitsmoment und mit welcher Drehzahl das Getriebe betrieben werden kann, wie breit die Kurve mindestens sein muss und welcher Geradenanteil im Bewegungsgesetz erforderlich ist.
Alle Ergebnisse werden kompakt und übersichtlich zusammengefasst.
Hier ein Beispiel für eine solche Auswertung:
Spreizen
Spiel ist für Getriebe aller Art schlecht, besonders bei hohen Taktzahlen:
- Bei Spiel ist die Lage des Abtriebsglieds nicht definiert, sie kann im Rahmen des Spiels schwanken. Das Getriebe erfüllt seine Positionieraufgabe damit nicht präzise.
- Spiel führt zu Stößen zwischen Rollen und Kurvenflanken bzw. ganz allgemein zwischen Antriebs- und Abtriebsglied. Stöße bedeuten Verschleiß und Lärm. Stoßweise Belastungen wirken zerstörerischer als kontrollierte, harmonische Belastungen.
Von den konjugierten Kurvenscheiben (auch Doppelkurven, Komplementärkurven, Haupt- und Gegenkurven, Arbeits- und Rückholkurve genannt) kennt man das in der Praxis verbreitete Verfahren, das durch Fertigungs- und Montagefehler entstehende Restspiel aus dem Getriebe herauszudrücken, um möglichst gute Laufeigenschaften zu erzielen. Bei Kurvenscheibenpaaren verwendet man dazu oft Exzenterbolzen oder ähnliche Verstellmöglichkeiten für eine Rolle.
Bei Globoidschaltkurven funktionieren Exzenterbolzen nicht. Das Spiel kann bei Globoidkurven-Schrittgetrieben über den Achsabstand eingestellt werden (siehe oben). Normalerweise möchte man den Achsabstand als wichtigste kinematische Abmessung aber fest haben, ohne Verstellmöglichkeit.
Um das Spiel aus dem Getriebe zu nehmen, können auch die Kurvenflanken in definierter Weise mit Aufmaß versehen werden. Die Kurvenflanken werden "gespreizt". So werden die Rollen auf dem Abtriebsglied in kontrollierter Weise um ein definiertes Maß auseinander gedrückt.
Globoidschaltkurven werden in Form einer oder mehrerer Nuten mit jeweils zwei Kurvenflanken hergestellt. Wenn eine der Flanken mit Aufmaß versehen wird, muss die Gegenflanke entsprechend zurückgenommen werden, damit die Rolle nicht eingeklemmt wird. Für das Aufmass kann man sich aber eine der beiden Flanken aussuchen, so dass die Rollen sowohl nach innen als auch nach außen gedrückt werden können.
Durch die Spreizung werden die Rollen gegeneinander verspannt, und es entstehen zusätzliche statische Kräfte zwischen Kurve und Rolle. Je größer das Aufmaß und je steifer die Rolle inklusive Lagerung, desto größer die zusätzlichen Kräfte. Deshalb sollte das Aufmaß so klein wie möglich gewählt werden, gerade so, dass das maximale durch Fertigung und Montage erwartete Spiel ausgeglichen wird.
Die folgende Animation veranschaulicht das Prinzip des Spreizens.
Dargestellt ist die Abwicklungsdarstellung eines Globoidkurvengetriebes für eine konstante Übersetzung.

In grau sehen Sie die theoretischen Kurvenflanken, und in weiss die tatsächlich berechneten Kurvenflanken, wie sie hergestellt werden sollen. Es ist erkennbar, dass die Kurvenrollen an den theoretischen Kurvenflanken gerade anliegen, in die tatsächlich hergestellten aber eindringen. Im realen Getriebe werden die Kurvenflanken die Rollen dann nach außen drücken und gegeneinander verspannen.
Kleine Anmerkung: Mit dem Aufmaß haben wir hier total übertrieben, damit man den Effekt in der Animation überhaupt noch sieht. In der Praxis geht es um sehr kleine Aufmaße.
Bei Zylinderkurven-Schrittgetrieben ist die Spreizfunktion in gleicher Weise anwendbar. Hier finden Sie eine 3D-Animation dazu, die das Spreizen plastischer zeigt.
Freischneiden
Bei der Herstellung und der Montage von Kurvenschrittgetrieben wird man geringfügige Maßabweichungen nicht vermeiden können, z.B. was die Lage der Rollen auf dem Rollenstern betrifft, die Rollendurchmesser, die Winkligkeit der Rollenachsen, den Achsabstand usw.
Diese Abweichungen zusammen mit dem Versatz aus dem Spreizen führen dazu, dass die Rollen beim Eintritt nicht perfekt tangential zur Kurvenbahn in den Kurvenkörper einlaufen, sondern mit einem geringfügigen Versatz.
Beließe man es bei den theoretisch berechneten Nuten inklusive Spreizen, aber ohne weitere Anpassung, so würden die Rollen beim Eintritt in den Kurvenkörper auf die Kanten stoßen, die durch den Schnitt zwischen Kurvenflanken und Kurven-Stirnseiten entstehen. In der Abwicklung sind das die spitzwinkligen Ecken zwischen linker bzw. rechter Stirnseite und den Kurvenbahnen. Diese Stöße bewirken Lärm, Verschleiß und insgesamt eine Verringerung der Lebensdauer der Kurvenrollen.
Wenn man weiß, wie groß die Fertigungs- und Montageabweichungen in Bezug auf die relative Lage zwischen Rolle und Kurve werden können, kann man an den Rändern der Kurve entsprechend große Einlauftrichter vorsehen. Dabei werden die Kurvenflanken über einen gewissen Winkelbereich etwas zurückgenommen. Die Profilrücknahme ist an den Kurvenrändern maximal und geht im Einlaufbereich stetig und ohne Ecken auf 0 zurück.
Die Rollen werden durch eine sich auf das Breiten-Nennmaß verjüngende Nut quasi sanft eingefangen.
Eine Animation zeigt dies für ein Globoidkurven-Schrittgetriebe in der Abwicklungsdarstellung.
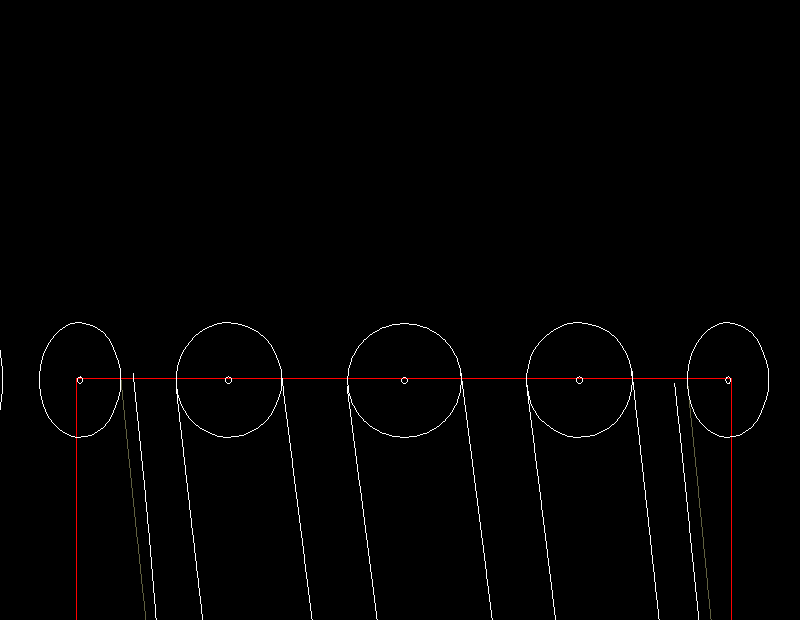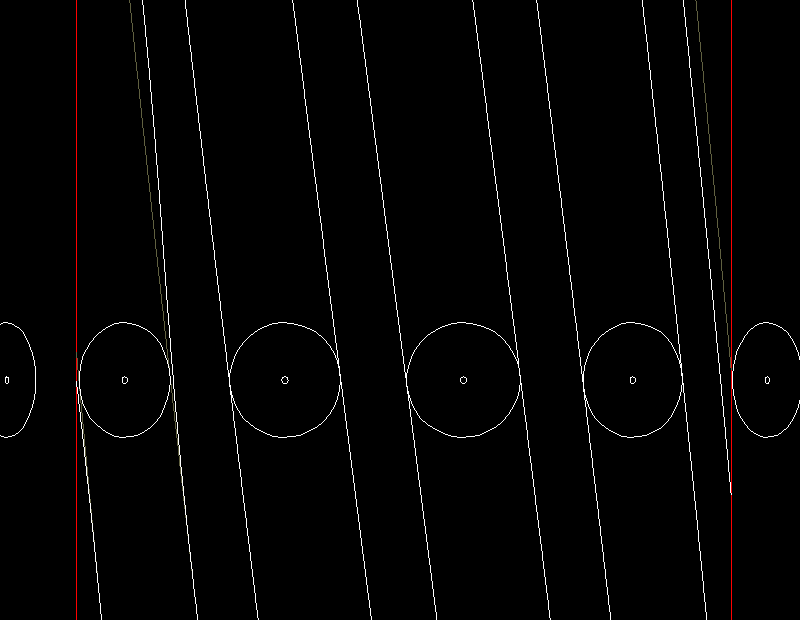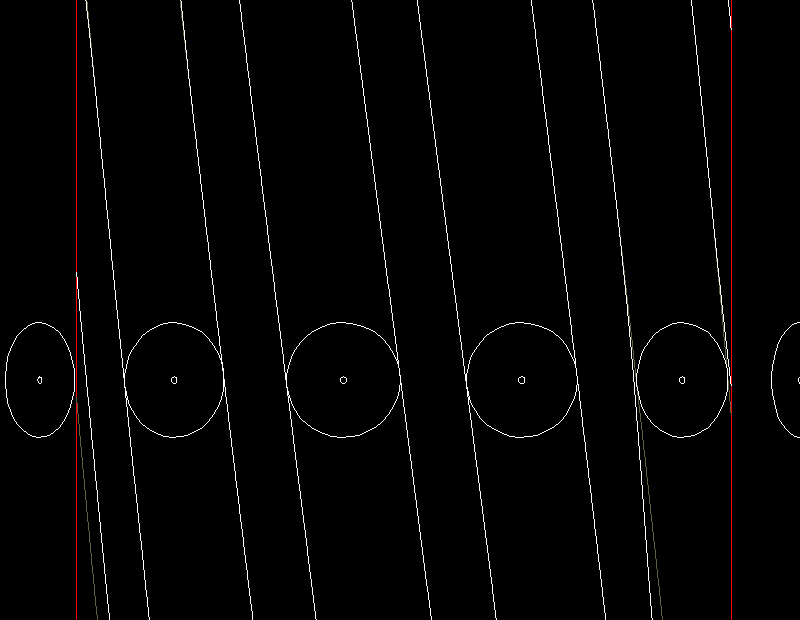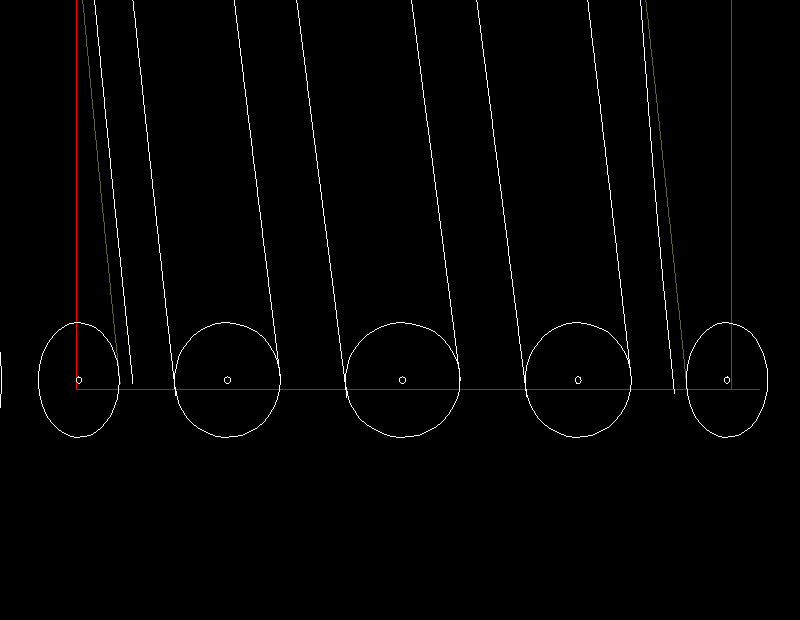
Grau dargestellt sind die theoretischen Kurvenflanken ohne Freischneidungen, in weiß sind die tatsächlich hergestellten Kurvenflanken mit Profilrücknahmen dargestellt. Die Toleranz für die Freigängigkeit der Rolle in der Nut wird hier nicht berücksichtigt. Man erkennt, dass die Rollen in der Mitte der Kurve an beiden Kurvenflanken anliegen, während sie an den Rändern der Kurve einen deutlichen Abstand davon haben.
Anmerkung: Auch hier haben wir mit dem Betrag der Profilrücknahme mächtig übertrieben, damit man sie noch erkennt.
Freischneidungen werden oft mit dem Spreizen der Kurvennuten kombiniert.
Bei Zylinderkurven-Schrittgetrieben werden Freischneidungen in den Ein- und Auslaufbereichen genauso verwendet. Hier finden Sie eine plastische 3D-Animation dazu.
Ausrundungen
Beim Fräsen von Globoidschaltkurven entstehen an Eintritt und Austritt der Kurvennuten spitz- und stumpfwinklige Kanten, die in der Praxis oft mit der Flex abgerundet werden.
Die NC-Postprozessoren von OPTIMUS MOTUS bieten Optionen an, um Ausrundungen unterschiedlicher Typen und definierbaren Rundungsradien direkt in die erzeugten NC-Daten zu integrieren. Die NC-Programme enthalten dann nicht nur Programmsätze für die Herstellung der eigentlichen Kurvenflanke, sondern auch der Ausrundungen.
Das Bild zeigt verschiedene Ausrundungstypen, die berücksichtigt werden.
Fasen
Die Grate, die beim Schneiden der Kurvenflanken von Globoidschaltflanken stehenbleiben, werden in der Praxis oft manuell mit Feile oder Flex entfernt. Trotz hohen Aufwands ist das Ergebnis nicht sehr schön.
Entsprechende Postprozessoren in der Software OPTIMUS MOTUS erzeugen NC-Daten für Entgratwerkzeuge, um die Globoidkurvenflanken maschinell zu entgraten.
Sie erhalten saubere, gleichmäßige, Fasen mit definierter Breite. Bei geringen Kosten haben Sie so ein hochwertiges Ergebnis.
Gangverkettung
Bei mehrgängigen Schaltkurven verbindet die Software OPTIMUS MOTUS die NC-Daten der einzelnen Gänge automatisch zu einem Gesamt-NC-Programm für alle Gänge.
NC-Optimierung
Kurven für Globoidkurven-Schrittgetriebe werden fünfachsig bearbeitet. Die klassische Strategie, mit Werkzeugdurchmesser = Rollendurchmesser zu schlichten, ist teuer, weil immer Maßfräser beschafft werden müssen, die je nach Getriebebaugröße auch noch unterschiedliche Durchmesser haben müssen.
Unsere Software OPTIMUS MOTUS berechnet auch für Globoidkurven eine Werkzeugradius-Korrektur und erzeugt NC-Daten entweder direkt für einen definierten Werkzeugdurchmesser oder - mit Hilfe der Parameterprogrammierung - für variable Werkzeugdurchmesser. Der konkrete Werkzeugdurchmesser kann dann noch an der CNC-Maschine eingegeben werden.
Diese Postprozessor-Option in OPTIMUS MOTUS spart bares Geld bei der Werkzeugbeschaffung.
Beim Schneiden einer Globoidkurvenflanke mit einem Standardwerkzeug bleibt theoretisch zuviel Material stehen. Die Profilabweichungen wachsen mit der Kurvensteigung, der Flankenhöhe und der Differenz aus Rollen- und Werkzeugdurchmesser. Wir schätzen die Abweichungen rechnerisch ab, um sicher zu gehen, dass die Kurve mit dem vorgesehenen Standardwerkzeugdurchmesser präzise genug hergestellt werden kann.
Darüber hinaus optimiert die Software die NC-Daten auf Wunsch numerisch nach, so dass die Fertigungsabweichungen auf ein Minimum sinken.
zur Startseite von Nolte NC-Kurventechnik GmbH
Start Fachberichte Mechanismen Kinematik Kurvengetriebe Schrittgetriebe Servo/SPS Bewegungen Fortbildung Software Service Kurvenberechnung Impressum Datenschutz
Varianten Auslegung Spreizen Freischneiden Ausrundung Fasen Gangverkettung NC-Optimierung
11/06/21
• Software OPTIMUS MOTUS ® /
DasNolte ®
• Berechnung von Kurven aller Art
• Performance-Optimierung
• Trainings und Beratung
• App- und Software-Entwicklung
• SPS-Bewegungsprogramme
Kurven, Mechanismen, Bewegungsdesign. Für schnellere Maschinen. Seit 1965.

